Computation Of Temperature Distribution On A Composite Aircraft Skin Protection Grid Due To Induced Electric Current During Flight under Thunderstorm Conditions

Keywords

Magnetic Field; Stepped Leader; Electric Current; Composite Material; Aircraft Skin; Protection Grid; Thunderstorm.

List of Symbols

c = specific heat of the heated material (J/m/C); dT = temperature rise due to power dissipation (C); I = electric current intensity (A); m = mass of the heating substance (kg); MAMB = Local ambient magnetic field strength (T) MDIST= disturbance magnetic field strength caused by the aircraft (T); R = protection grid wire electric resistance (Ω); t = time interval (s); μ = heating efficiency; ρ = resistivity of the material of the grid (Ωm).

Introduction

In recent years,composite materials saw a widespread use in aircraft manufacturing for empty weight savings. The drawback of these materials is their vulnerability in lightning strikes due to a poor thermal and electric conductivity. To overcome this issue, some solutions are adopted such as full or local aluminum coating and aluminum or copper grid fully imbedded into the composite material [1, 2].

In case of flight in a region where an ambient magnetic field is present, such as in a thunder cloud region, according to Lenz law [3] an electric current is created and circulates along the sides of all meshes of the grid. This current produces heat everywhere on the grid, which is transferred to the composite material.

Thunderclouds are usually present at altitudes up to 600 m to 900 m, so low altitude flight is concerned. A lightning spark from such a cloud to the ground can be considered as a wire traversed by an electric current with a peak of several hundred of Ampères [4]. This way an ambient magnetic field is created. In this paper, a method for computing the temperature distribution inside a composite aircraft skin due to the presence of an ambient magnetic field is presented. This method is based on Biot - Savart [3] and Lenz laws. The temperature distribution corresponds to the highest intensity peak in a lightning flash.

Presentation of the Approach

Aglobal frame is tied on the aircraft. The origin of this frame lies on the nose of the aircraft, the x-axis is on the longitudinal axis and directed towards the tail. The y-axis, parallel to the span, points to the right wing according to the pilot's view. The z-axis is normal to the x - y plane and pointssuch that the global frame is a right orthogonal one.

The thickness of the composite material is negligible as compared to the aircraft dimension, like fuselage diameter or lifting surfaces thickness. Since the grid is embedded into the composite material it can be assumed that all grid points describe very accurately the aircraft geometry. Based on this, the external surface of the airplane is described by a number of points, the coordinates of which are expressed in the global frame.In this study, the entire aircraft is considered to be made from composite materials.

These points represent the grid points and are combined by three or four to form panels, while each panel is consider as a plane one. The number of points should be sufficient so as to accurately describe the surface of the aircraft. Then, the coordinates of the centroid G of each panel, the local (panel) frame G, t , l , n → → → , the midpoint of each side GM common of two adjacent panels and the length of each common side for all panels are calculated. The unit vectors of the axes of the panel frame, namely n → (normal unit vector pointing outwards),t → and l → (tangent vectors to the panel surface) are such that the panel frame is also a right orthogonal one.

Lenz law states that an induced electric currentis trying, by its electromagnetic effect, to cancel the cause which creates it. This means that along the sides of all meshesof the web, i.e. the sides of each panel, an induced electric current will be induced, which in turn will create a disturbance magnetic field so as to cancel the ambient one. According to Lenz law, the ambient magnetic field M → AMB and the disturbance magnetic field M → DIST should satisfy everywhere the following condition (equation 1):

EQ (1,2)

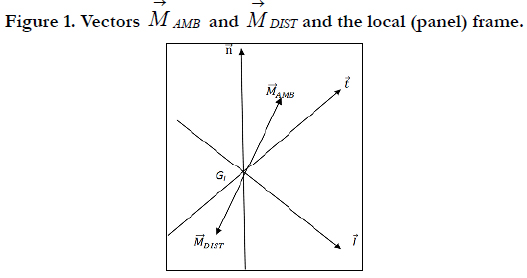
Figure 1 shows vectors DIST M → and AMB M → and the local panel frame G, t , l , n → → → . All vectors in figure 1 are expressed in the global frame.

As it is shown in figure 1, two mixed products can be formed. Since a mixed product represents a volume, equation (2) is satisfied only if the volumes represented by the mixed products are equal (equation (3)).

EQ (3)

In equation (3) MDISTX, MDISTY, MDISTZ, MAMBX, MAMBY and MAMBZ are the component of DIST M → and AMB M → in the global frame. MDISTX , MDISTY, MDISTZ respectively are equal to (equations 4):

Ij is the induced current intensity circulating along the sides of panel j and mXIJ, mYiJ and mZiJ are the components of the magnetic field induced at the centroid of panel I by a unit electric current circulating in all sides of panel j . These component are calculated according to the Biot - Savart law.

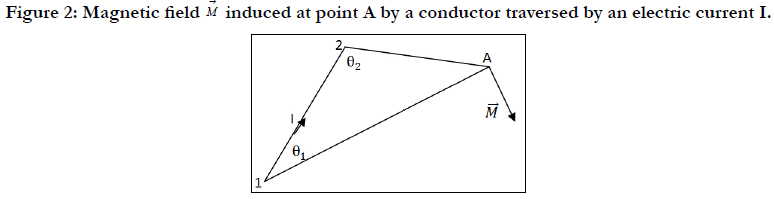
The Biot - Savart law states that a rectilinear electric conductor traversed by an electric current I, induces at a point A a magnetic field M → , (figure 2). The module of M → equals to (equation 5):

EQ (5)

In equation (5), μ0 = 4π10-7 Tm/A is the magnetic permittivity of the air and d is the distance of point A from the conductor.Vector B → is normal to the plane formed by the rectilinear conductor and point Aand points according to Maxwell rule, in this case as shown in figure 2. It must be pointed out that the Biot - Savart law is also used in potential flow aerodynamics where the roles of I and B → are played by the vorticity Γ and the induced velocity V → respectively [5].

Equations (3) and (4) combined are giving the boundary condition to be satisfied at any panel centroid (control point) Gi on the aircraft skin.

By applying this boundary condition, to the centroid of N panel, a system of N x N linear algebraic equations is obtained. The solutions of this system are the values and the sign of theelectric current intensity Ij due to M → AMB and circulating on the sides of allpanels approximating the external surface of the aircraft. This computation is made using a modified in house aerodynamic computer code, based on 3D vortex lattice method [5].

Once the value of I everywhere on the grid is computed, the corresponding temperature rise, in Celsius degrees, can be calculated. The expression of the temperature rise in a given material is expressed by (equation 6, [9]).

where

R = electric resistance of the grid material (Ω), I = electric current intensity (A), t = time interval (s), μ = heating efficiency, c = specific heat of the heated material (J/m/C) and m = mass of the heating substance (kg).

The electric resistance R is given by equation (7):

where

ρ = resistivity of the material of the grid (Ωm), L = length of the conductor (m) and S = section area of the conductor (m2).

Results

A generic airliner geometry of 50 m fuselage length and 60 m wing span is created. The linear algebraic equation system is solved using a singular value decomposition method [6]. The aircraft was in level flight and exposed to an ambient magnetic field of various strength. This ambient magnetic field is considered as parallel to the x-axis of the global frame.

As it was already said at the introduction, a lightning from a thundercloud to the ground is approximated by a straight wire of length equal to 900 m and traversed by an electric current of an intensity peaking up to several thousand of Ampères, actually up to 200000 A [8]. The intensity of the induced magnetic field at various distances from the lightning and various flight altitudes up to 900 m can be calculated according to Biot - Savart law. In table 1, the strength of the ambient magnetic field at various distances (500 m, 1000 m and 1500 m) from the lightning and at 450 m of altitude are presented.

These values are to be compared to the magnetic field of the Earth which varies from 25.10-6T to 65.10-6 T [7] and obviously in all cases MAMB is stronger.

In this study the grid is assumed to be made of aluminum so, c = 890 J/m/C and ρ = 2,65.10-8Ωm [10]. L is the length of the common side of two adjacent panels of the grid. The density of the aluminum equals to 2700 kg/m3. Since no data about the grid wire diameter could be found, a typical fusel age skin thickness was taken, in this case concerning a Boeing 787 with a skin thickness of 0,99 mm. According to this, the grid wire diameter was taken equal to 0,50 mm. In this case there is an electrical heating, soμ =1. According to [8], the velocity to the ground of a step leader is about 1,5.105 m/s. As it was already said in the introduction, since thunderclouds altitude is up to 900 m, the duration of the lightning flash is estimated at 0.006 s. Assuming that the induced electric current will last as long as the lightning flash exists, t = 0.006 s.

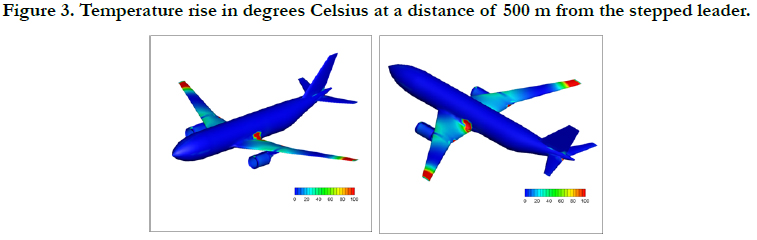
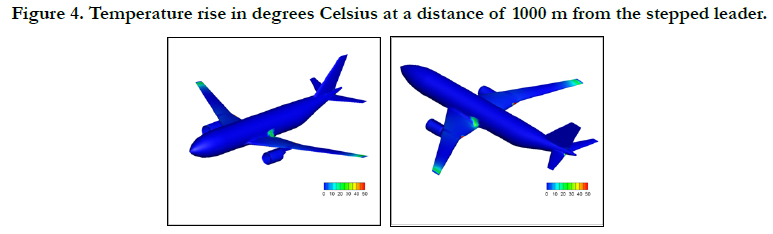
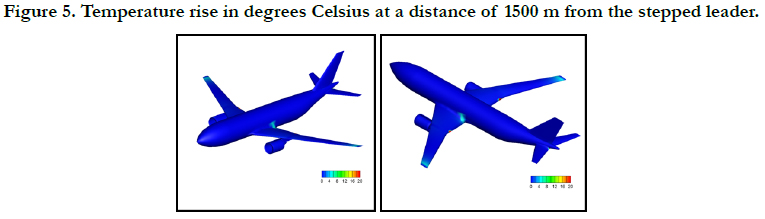
Based on this, in figures 3, 4 and 5 the temperature rise distribution in Celsius degrees inside the aircraft composite skin is shown for distances of 500 m, 1000 m and 1500 m from the lightning flash. In all figures, the color palette is modified in order to let the highest values be also visible. For this reason in figure 3, the red color corresponds to the value of 50 (maximum of the palette) up to the value of 8312 degrees C (maximum of the result file). In figure 4, the red color corresponds to the maximum of the palette up to the value of 781 degrees C. Same in figure 5, where the red color corresponds to the maximum of the palette up to the value of 70 degrees C.

The closer to the stepped leader the highest the temperature rise, as it was expected. On the other hand, in all cases, the wings seem to be more affected than the fuselage and the tail unit. This is due to the shape of the grid adopted here. It must be pointed out that, in this study, the same points which describe the surface of the aircraft define also the protective grid so that, the sides of the panels on the surface of the aircraft are forming also the mesh of the grid.

According to [11], the melting temperature of the carbon fiber varies from 3652 to 3697 degrees Celsius. This means that at some points the skin might be melted and cracks be formed. The length of these cracks equals the length of the wire of the grid beneath them. On the other hand, flight too close to a stepped leader is not frequent. In order to clarify this problem, a structural analysis should be made to investigate if these local damages have an impact on flight safety in along term and how frequently they must be monitored.

×

Figure 1

Close

Figure 1. Vectors AMB M → and DIST M → and the local (panel) frame.

×

Figure 2

Close

Figure 2: Magnetic field M → induced at point A by a conductor traversed by an electric current I.

×

Figure 3

Close

Figure 3. Temperature rise in degrees Celsius at a distance of 500 m from the stepped leader.

×

Figure 4

Close

Figure 4. Temperature rise in degrees Celsius at a distance of 1000 m from the stepped leader.

×

Figure 5

Close

Figure 5. Temperature rise in degrees Celsius at a distance of 1500 m from the stepped leader.

×

Table 1

Close

Table 1: Ambient magnetic field strength calculated at various distances from the lightning at a flight altitude of 450 m.

Conclusions

In this paper a numerical approach is presented, aiming to calculate the temperature rise distribution along all meshes of a metallic grid embedded in the composite skin of an aircraft. This knowledge permits to spotan immediate damage of the composite skin due toa local high temperature rise, even of extremely short duration. According to the results obtained, in some points the temperature rise will locally make the composite structure to melt. Of course, in this paper only the method is presented and the same computation must be repeated based on the exact geometry of the protecting grid of a real aircraft not on a generic one. It must be established if a very local damage can compromise in long term the stability of the entire structure, despite the low frequency of occurrence of a flight too close to a stepped leader.

Acknowledgment

The author wish to thank the Parallel CFD and Optimization Unit of the Department of Mechanical Engineering of the National Technical University of Athens for its assistance in the post - processing of the results.