The Variation Of The Natural Frequencies With Increasing Pure Shear Loads For Rectangular Isotropic Plates

Keywords

VCT, Buckling; Thinwalled Isotropic Rectangular Plate; Natural Frequencies; Relationship Between Frequencies Squared And Applied Shear Load.

Introduction

Thin walled structures, like columns, plates and shells are liable to buckling when subjected to axial compressive loads. Although the buckling loads of those basic structures can be analytically calculated, their experimental values are found to be less than the numerical predictions. This is due to the real boundary conditions of the tested specimens, the initial imperfections of the structure and the load eccentricity induced during the tests. Not all those factors can be a priori taken into account, leading to over prediction of the buckling loads using analytical formulas of by modeling the thin structure with a finite element code. The discrepancy between the experimental and numerical/analytical predictions leads to the including of a knockdown factor (less that unity). This factor multiplies the numerical/analytical buckling load value to yield a design buckling value for the thin walled structures. As the knockdown factor is based on the lower value for all the experimental results included in the database for a certain thin walled structure, the resulting structure will have higher thickness, thus reducing its stiffness/mass advantage. The striving of an engineer is to be able to nondestructive predict the actual in-situ buckling loads of a thin walled structure, and thus save weight of the structure. One of those methods is the VCT (vibration correlation technique).

The vibration correlation technique (VCT) consists of measuring the natural frequencies of a loaded structure, and monitoring their change, while increasing the applied load. Assuming that the vibrational modes are similar to the buckling ones, one can draw a curve, displaying the natural frequencies squared vs. the applied load, and extrapolating the curve to zero frequency would yield the predicted buckling load of the tested structure. In [1] Abramovich, dedicated a whole chapter in his book, to review the VCT approach and its applications. The subject was also presented in details in [2].

Besides its capability to nondestructively predict the buckling load of thin walled structures, the approach can also determine the actual in situ boundary condition of the structures, and therefore the VCT is usually classified in two main groups according to their approach: (1) determination of in situ boundary conditions, and (2) direct prediction of buckling loads.

The VCT method has been successfully applied to beams and columns axially loaded, (see for example Refs.[2-17]), yielding a straight line between the frequency squared and the compressive load for both theoretical and experimental cases. Taking into account the differential equation for an isotropic column with constant properties EI along its length L, compressed by an axial loading P and undergoing small vibrations at a circular frequency ω, which can be presented as:

one can easily find the buckling load Pcr and its fundamental frequency f1 for a column on simply supported boundary conditions. Their relevant expressions are



where ρA is the mass per unit length. Using the definitions in Eq. 2, it is easy to find the following relationship between the compressive load and the natural basic frequency of the column:



where f and f1 are the measured frequency and its value at zero compressive load, respectively and p and Pcr are the experimental applied compressive load and its buckling value at zero frequency, respectively.

One should note that other cases of columns, like a compressed column on Winkler-type foundation, laminated symmetric and non-symmetric compressed columns using either CLT (Classical Lamination Theory) or FOSDT (First Order Shear Deformation Theory) theories [1] would also comply with the expression presented by Eq.3.

The application of VCT on perfect plates and shells, for compressive loading has also being dealt in the literature as presented in Refs. [17-26] and [27-44], respectively. For perfect rectangular isotropic plates the differential equation of motion can be written as [1]



where E is the Young' modulus, h=plate thickness and ρh=mass per unit area of the plate.

Nx and Ny are the in-plane loads per unit length in the x and y directions, respectively.

For a simply supported all around case, one obtains the following expressions for the natural frequencies and the buckling loads for compression in the x only or y only directions:



Keeping in mind the expressions in Eq. 5, and using Eq. 4 one obtains the following equation



which is similar to Eq. 3, namely the frequency squared is linearly dependent on the compressive loads, as was shown above for columns. This linear equation was shown to be also true in experiments, see for example [18]. However, as in real life plates have some initial imperfections, the theoretical linear relationship cease to be true as the compressive load is approaching the buckling load [21]. At the buckling load, which does not occur at zero frequency, and afterwards, the curve starts to raise again with the increasing of the compressive load. Experimentally, the point where the curve changes its tendency would be the VCT predicted buckling load.

As pointed out in [1, 2], also for cylindrical shells compressed axially a linear theoretical curve exists for the square of the lowest natural frequency and the applied compressed load. However, when trying to apply the VCT to a cylindrical compressed shell, the linear relationship predicts higher and wrong buckling loads. The literature presents two applications to correctly predict the buckling loads of cylinders. The first one is attributed to Souza et al. [30-32] that suggested using the following relationship



where ξ is the “experimental” knock-down factor based on the results of the test, at relatively low loads. The procedure starts with the acquisition of the natural frequencies at zero axial load. Then the load is increased and the nondimensional frequency f is calculated for each load step, by normalizing the measured frequency at a compression load P by the frequency at zero compression. Then the load P is also normalized by the numerical buckling load Pcr to yield the variable p. At about 60% of the calculated buckling load the test is stopped, a straight line is drawn, starting at point [(1-f4)=0,(1-p)2=1] till point (ξ2,(1-f4)=1]. The value of ξ2 is determined as thecross point between the oblique line and the vertical line from (1-f4)=1. The application of Eq. 7 was shown to provide good results for stringer stiffened circular isotropic shells [30]. Another application is the empiric relationship suggested by Arbelo et al. [34, 35]. The empirical approach is based on the modification of Eq. 7 yielding the following relationship



Then a graph of (1 - p)2 vs. (1 - f2) is constructed based on a typical test. Following the definitions of p and f, presented in Eq. 7, a best fit second order equation is approximated based on the experimental points. The fitted second order polynomic curve of the measured experimental natural frequencies would have the following expression:



with the values of the constants α, β and χ being determined by the best fit process. Finding the minimal point of the second order equation presented in Eq. 9 yields



with ξ being the "knock-down factor" which represents the drop in the shell load carrying capacity, like Souza et. al [30] method, presented above, leading to the prediction of the in-situ tested specimen using the following form:



The use of Arbelo's empirical method provided very good results, as shown in Ref. [33-44].

When trying to apply the VCT to plates loaded in pure shear ,due to the complexity of the problem , the linear relationship presented before does not hold anymore, and a new procedure should be used. The influence of shear on the natural frequencies of a flat plate was rarely treated in the literature (see [45-60]) with no decisive formulation. Therefore, the present study is intended to provide an application aimed to allow predicting the buckling of a flat plate under pure shear, by monitoring its natural frequencies.

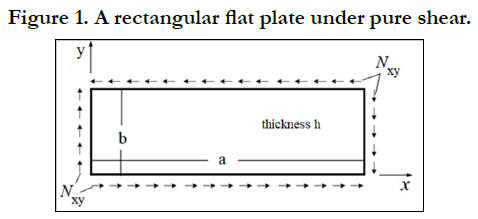
A flat isotropic plate under shear

Figure 1 presents a rectangular isotropic flat plate, having the thickness h, length a and width b under shear loads Nxy per unit length.

The differential equation for this case can be written as



Due to its problematic appearance of Eq. 12, there is no closed form expression for the critical shear (or shear stress) loading. Only approximate solutions are available in the literature. One of those solutions is the one presented by Timoshenko & Gere [61] and can be presented as



The factor k depends on the aspect ratio (a/b) on the flat rectangular plate as presented in Table 1 (from [61]).

For larger aspect ratios, the following approximation should be used (see [61]):



The natural frequency expression for the unloaded case keeps it value as it was shown above in Eq. 5.

To investigate the relationship between the shear load and the natural frequency of a flat rectangular plate, a finite element model using ANSYS Workbench 2020 (Student Version) [62] was constructed and its results are next presented.

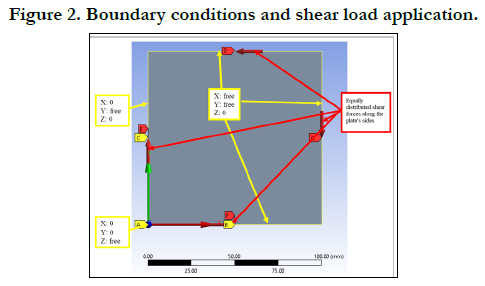
The finite element model consists of a 100 x 100 mm2 plate with a thickness of 1 mm. The chosen material has a Young's modulus of 200 GPa, a Poisson's ratio of 0.3 and a density of 7850 kg/m3. The basic square model had 50 x 50 Quad elements. To enable simulations for various aspect ratios (AR=a/b) the basic model was enlarged in the x direction, yielding 50*AR elements. Figure 2 presents the application of the shear forces and the applied boundary conditions to simulate the demanded simply supported all around the plate circumference.

Results

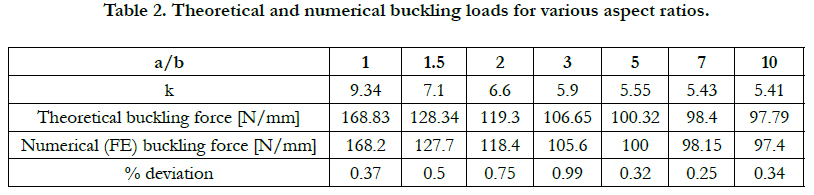
The buckling load calculated by the finite element code are presented in Table 2 for various aspect ratio of the plate and compared to the theoretical values obtained thru Eqs.13 and 14.

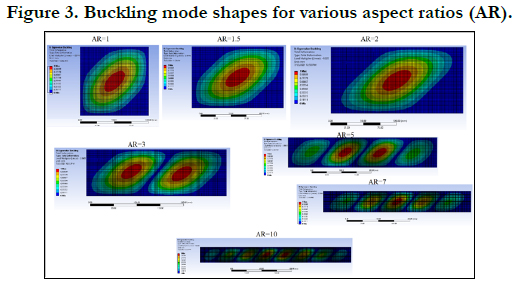
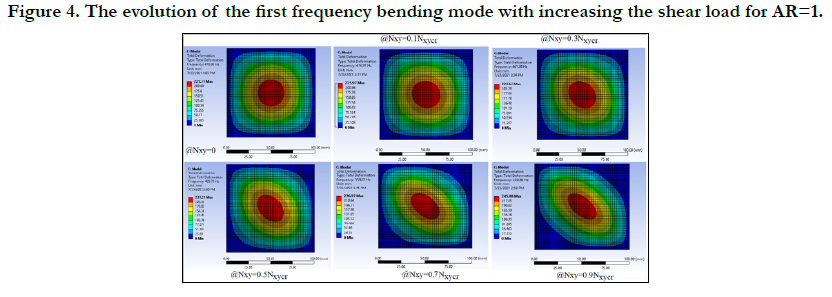
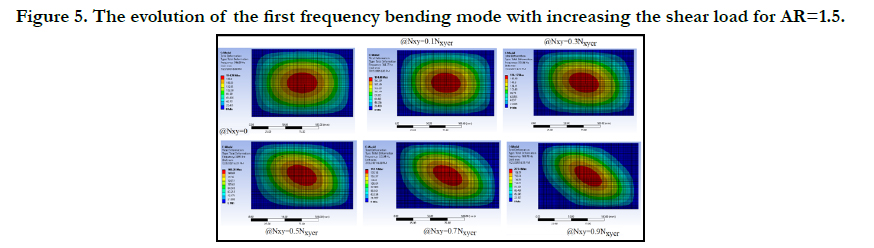
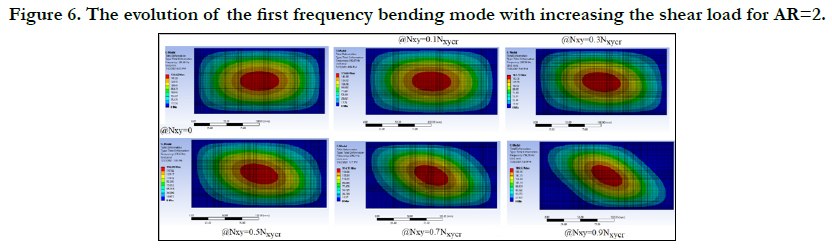
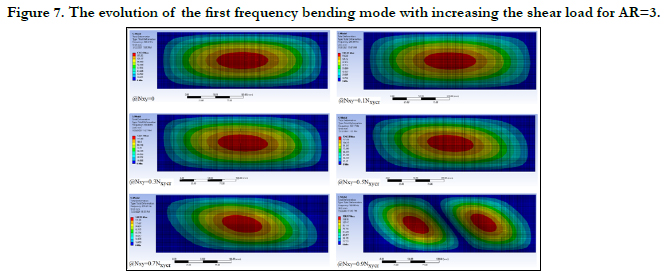
As one can see, the results from the finite element code are in very good agreement with the theoretical ones, the largest deviation being 1% for AR=3. The buckling mode shapes are presented in Fig. 3. Next, the natural frequencies for various levels of the shear load were calculated and presented in Figs. 4-7, for AR=1, AR=1.5, AR=2 and AR=3, respectively.

As can be seen from Figs. 4-7, the first frequency mode of bending changes its shape and rotates along the main diagonal line of the plate's surface, till its shape is identical to the buckling mode shape (see Fig. 3). Note the interesting phenomenon presented in Fig. 6 , where for an aspect ratio of AR=3, the frequency mode shape changes it shape from one a single oblique half at 70% of FE buckling load wave to two oblique half waves at 90% of the FE buckling load, which is the exact buckling mode as displayed in Fig. 3.

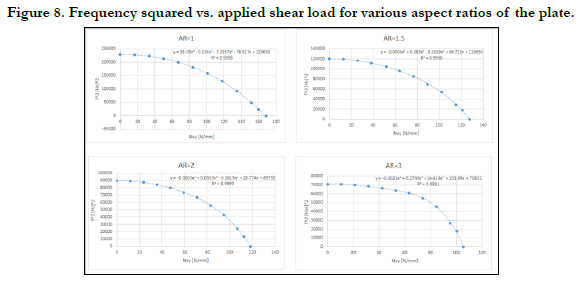
Figure 8 displays the variation of the frequency squared with the increasing of the shear load, for aspect ratios of AR=1, 1.5, 2 and 3. The fourth order polynomial equation fitted to the FE calculated values is presented for each graph and includes its relevant R2 value (how good is the fitted polynomial equation for the given data, with R2=1 been a 100% fitting).

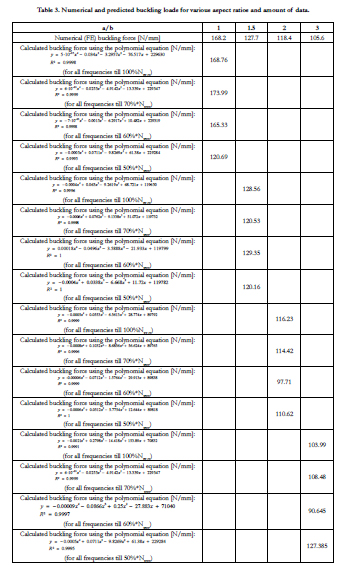
The calculated buckling loads, using the various fitted polynomial equations are presented in Table 3, together with the referencebuckling load, as calculated by the FE code.

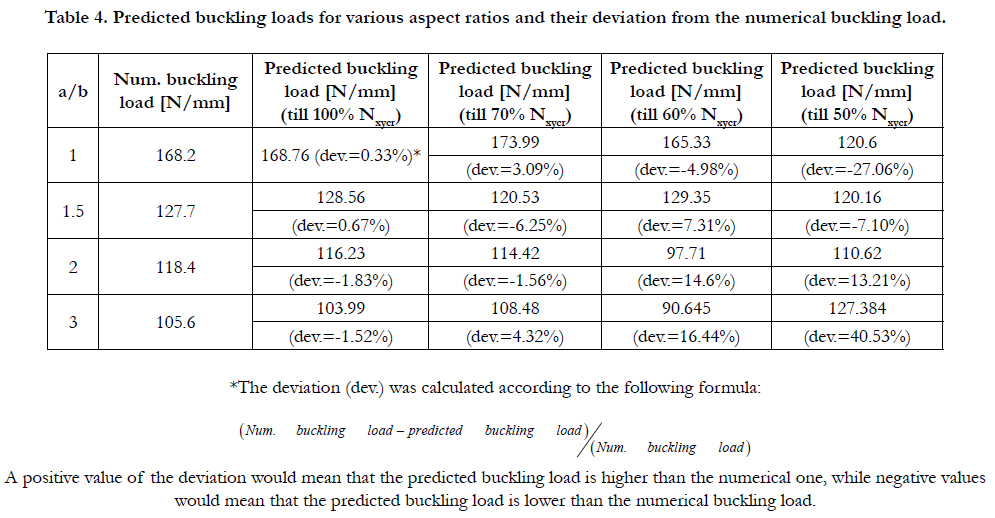
Table 4 presents the various deviations of the predicted buckling loads from its relevant numerical buckling loads for various aspect ratios. One can see that the predicted buckling loads when taken into account 100% Nxycr of the points are in a very close proximity with the numerical buckling loads (deviations between 0.33% and -1.83%). However, the prediction procedure should use much less points to be used as a VCT approach. As is depicted in Table 3, taking into account 70% Nxycr points also leads to a good proximity to the numerical buckling loads (deviations between -1.56% and 4.32%). This proximity deteriorates for points up to 60% Nxycr (deviations between -4.98% and 16.44%) and up to 50% Nxycr (deviations between -7.10% and 40.53%).

Based on the above results, to use the present method as a VCT approach, it is recommended to use points up to 60% or 70% of the calculated buckling loads.

×

Figure 1

Close

Figure 1. A rectangular flat plate under pure shear.

×

Figure 2

Close

Figure 2. Boundary conditions and shear load application.

×

Figure 3

Close

Figure 3. Buckling mode shapes for various aspect ratios (AR).

×

Figure 4

Close

Figure 4. The evolution of the first frequency bending mode with increasing the shear load for AR=1.

×

Figure 5

Close

Figure 5. The evolution of the first frequency bending mode with increasing the shear load for AR=1.5.

×

Figure 6

Close

Figure 6. The evolution of the first frequency bending mode with increasing the shear load for AR=2.

×

Figure 7

Close

Figure 7. The evolution of the first frequency bending mode with increasing the shear load for AR=3.

×

Figure 8

Close

Figure 8. Frequency squared vs. applied shear load for various aspect ratios of the plate.

×

Table 1

Close

Table 1. Variation of the k factor with plate aspect ratio, a/b.

×

Table 2

Close

Table 2. Theoretical and numerical buckling loads for various aspect ratios.

×

Table 3

Close

Table 3. Numerical and predicted buckling loads for various aspect ratios and amount of data.

×

Table 4

Close

Table 4. Predicted buckling loads for various aspect ratios and their deviation from the numerical buckling load.

Conclusions

A study was initiated to investigate the changes in the natural frequencies of flat isotropic rectangular on all around simply supported boundary conditions under increasing pure shear, till buckling. This case differs completely from the cases of plates under compressive loads for which the square of the natural frequency is inverselinearly to the applied compressive loads. The frequency squared for a plate under increasing shear shows a non-linear behavior, which should be defined. The results of the investigation for flat plates with aspect ratios of AR=1, 1.5, 2 and 3, show that:

• The relationship between the applied shear load and the frequency squared can be approximated using a fitted 4th order polynomial equation, when using frequencies from zero till buckling.

The deviation between the predicted buckling load and the calculated FE buckling load is very low and ranges from 0.33% to -1.83%.

• Using only part of the points, from zero to 70%Nxycr and fitting a 4th order polynomial equation, yield also good results with deviations ranging between -1.56% and 4.32%, which, from the engineering point of view can be considered a good tool to predict buckling under pure shear.

• Trying to reduce the points used to fit a 4th order polynomial equation up to 60%Nxycr or 50%Nxycr would predict buckling loads with large deviations (larger than 5%) from the numerical FE buckling load.

• It is recommended that the user would use points up to 70%Nxycr, to predict the pure shear buckling load of a flat isotropic rectangular plate on simply supported boundary conditions with a high level of confidence.

• It was observed that the first mode changes its shape during the increasing of the shear load and rotates to yield the inclined buckling mode of the plate under shear.

• Moreover, for an aspect ratio of AR=3, the one oblique half wave frequency mode, would jump to two inclined half waves frequency modes when applying 70% Nxycr and it keeps this form up to buckling under shear.

• One has to remember, that once geometric imperfections are taken into account, and the plate is no more flat, the equations of motion would change and the frequency squared vs. the applied shear load relationship might be different. For plates under compressive loads, experiments show that the frequency squared does not diminish to zero at the buckling load. Instead, the reduction of the frequency squared changes its tendency at the buckling load and starts increasing its value. The load, at which the curve changes its tendency, would be defined as experimental buckling load. This behavior is expected to appear also in experiments on plates under pure shear loads.