Keywords

Nozzle Flow; Flow Separation; Overexpanded; Planar Nozzle.

List of Words

A = local area [m2]; f = frequency [Hz]; L = length [m]; M = Mach number; M⋅ = mass flow rate [kg/s];P = pressure [Pa]; S = Strouhal number, (S = fL/U); U = velocity [m/s]; X* = normalized length of the diverging part of the nozzle, (X*=X/XNozzle), ρ = density [kg/m3]; NPR = nozzle pressure ratio, (NPR=P0/Pamb); Subscripts: amb = at ambient condition; e = at the nozzle exit; o = at stagnation condition; w = at the leading edge of the wedge; t = at the nozzle throat.

Introduction

Flow separation in convergent-divergent (CD) nozzles occurs when the dynamic pressure of the fluid in the boundary layer is not high enough to overcome the rising pressure ratio along the diverging part of the nozzle. This phenomenon has many engineering application aspects such as jet engine performance, noise from jet engines, limitations on the construction of rocket nozzles or thrust vectoring. Therefore, it is of interest to understand the physical aspects of the phenomenon. The inviscid quasi-one-dimensional equations of the flow in the divergent part of a CD nozzle indicate that as the area ratio (AR) increases the static pressure of the jet emerging from the nozzle decreases. Therefore, moving downstream towards the nozzle exit, the pressure ratio between the ambient pressure and the jet pressure increases [1]. If the pressure ratio between the stagnation conditions and the ambient is higher than that required to generate a sonic flow at the throat but not high enough to satisfy the isentropic relations, a normal shock will occur in order to resolve the pressure mismatch with the ambient conditions. As the stagnation pressure increases the location of the shock moves downstream until it reaches the nozzle exit. Further increase in the pressure ratio results in an oblique shock emanating from the lips of the nozzle.

Experiments revealed that this description is accurate only for the isentropic part of the flow and most often the shock wave that is formed is not a normal one. It is known that flow separation at low Mach numbers produces a typical formation, often termed as “lambda foot”, of a slightly convex Mach stem with a Mach reflection (MR) at its ends. As can be seen in Figure 1, at higher Mach numbers an oblique shock is generated from the opposite sides of the nozzle, and it is reflected at the symmetry plane as a regular reflection (RR). These flow separation structures are most often symmetric when the flow separation occurs close to the nozzle exit plane. However, when the flow separation occurs further upstream of the nozzle exit, it can become asymmetric or exhibit unsteadiness.

---

---

Summerfield et al. [3] reported that at low nozzle pressure ratios the flow separation in a planar nozzle was asymmetric, but no model was presented to explain this. Arens and Spiegler [4] showed a plot of stable and unstable flow regions at different Mach numbers and noted that unstable regions also exhibited asymmetric separations, but they offered no explanation of its origins.

As shown in Table 1, several investigators studied the occurrence of flow separation inside CD planar nozzles. A summary of their experimental and numerical observation is that the formation of the shock system starting at the separation point seems to be dictated by the nozzle exit area ratio and the separation Mach number. At low Mach numbers, an MR was formed with a nearly straight Mach stem, a triple point and a slip-line, while at higher Mach numbers an oblique shock with an RR was formed. The type of the reflection stayed the same regardless of whether the separation was symmetric or asymmetric. In all the cases in which the asymmetric separation contained a lambda foot; i.e., an MR with a triple point close to the wall, the flow did not reattach to the wall downstream of the separation point, but rather resulted in “small” and “large” separated regions. In the case of asymmetric oblique separation the flow attached to the wall up to the nozzle exit. The attachment of the flow appears to be related to the Coanda effect where the inability of the jet to entrain ambient fluid due to the proximity to the wall causes it to draw itself closer to the wall until it attaches to it [9]. When flow separation occurs in axisymmetric nozzles, two distinct types of separation process can be found. One is the Free-Shock-Separation (FSS), in which downstream of the separation point reverse flow takes place. The second is the Restricted-Shock-Separation (RSS) in which the flow reattaches to the wall downstream of the separation point creating a closed recirculation bubble [10, 11].

A research direction of particular interest entails investigating nozzles with exit AR in the range 2÷8, and separation Mach numbers above 2.2. To the best of our knowledge, no investigation into the mechanism of asymmetric flow separation in CD planar nozzles at high-Mach numbers has been reported. Previous studies [3, 4, 8] only noted the phenomenon as a peculiarity of the main topic of their investigation. It is known that the mechanism that initiates flow separation in axisymmetric CD nozzles is very similar to that in CD planar nozzles and that in both types of nozzle, asymmetric separation can occur. The issue of side loads in rocket nozzles at sea level conditions caused by asymmetric separation was thoroughly investigated by [12-14], but experimental work is difficult to conduct for two reasons: first, making a transparent nozzle for optical measurements is complicated and so is the interpretation of the produced images; second, due to the axisymmetric construction and the unsteadiness of the flow, the asymmetry can change position both azimuthally and axially.

Understanding the mechanisms that govern asymmetric flow separation in planar nozzles can promote our understanding of the phenomenon encountered in axisymmetric nozzles, as done by other investigators (see Table 1). As noted earlier, flow separation inside a planar nozzle can result in RR or MR, which have considerably different shock cell structures. The RR produces a wavy jet boundary that affects the wall pressure while the MR generates a rather straight jet, and thus, the pressure along the wall is steady [15]. The type of reflection that actually occurs depends on the Mach number upstream of the shock system and the pressure ratio across the oblique shock. If the point of reflection is outside the nozzle, the pressure downstream of the incident shock is equal to the ambient pressure while the pressure upstream of the shock depends on the stagnation pressure dictated by the isentropic relation. When the reflection point is inside the nozzle, the pressure downstream of the incident shock is generally lower than the ambient pressure and depends on its geometry and the structure of the shock cells. In the case of axisymmetric nozzles, flow separation at all Mach numbers should result in an MR, as an RR at the axis of symmetry is analytically impossible [16], but the Mach disk can be small enough so that the shock cell structure is similar to that of an RR [17].

---

---

Financial and time restrictions prevented us from designing and manufacturing several nozzles with different area ratios. To investigate flow separation in nozzles with varying Mach numbers, a wedge having the same half angle was inserted into a tapered nozzle at different stream-wise positions (see Figure 2). The location of the wedge determined the exit area of the nozzle and,in turn, the fully expanded Mach number. From the leading edge of the wedge to the nozzle exit two ducts with constant area were formed, and the flow was deflected by the wedge half angle. The advantage of using this method is that it enables a continuous change in area ratio during the experiment with a single nozzle. However, the length of the constant area ducts decreases as the wedge is pulled out.

---

---

Experimental Arrangement

The experimental study was conducted in the Hot Jet Facility of the Advanced Aero Propulsion Laboratory at Florida State University. The facility is designed to simulate the exhaust of jet engines and is able to produce stagnation conditions of up to 300 psi (2 MPa) and 2000°F (~1366 K) using an ethylene burner. The jet from the nozzle exhausts into a fully anechoic chamber whose main use is for studying jet noise. The jet is fed from a 2000- psi (13.8-MPa), 10-m3 pressure vessel and is regulated by twostage control valves to achieve long run times and stable pressure conditions. A 3” diameter flange protrudes into the anechoic chamber where it connects to a circular to rectangular transition block followed by a rectangular conduit with a set of double screens to reduce large-scale vortices. The conduit has ports for measuring the stagnation pressure and temperature. As the burner was designed to reach high temperatures, it could not be operated at stagnation temperatures below 450 K, and therefore, all tests were conducted with the burner off. During the test run the stagnation temperature dropped from 290 K to 283 K.

The nozzle used in the experiments was a planar (2D) tapered CD nozzle with an exit-to-throat area ratio of 8. The throat height was 3.175 mm (1/8”), the divergence half angle was 10°, and the radius of curvature ratio in the converging part was 16 to give a nearly straight sonic line. The diverging part of the nozzle was 65.25-mm long. The nozzle was constructed to allow the contoured faces to be replaced with minimal changes. The flange connecting the nozzle to the rectangular conduit was made of stainless steel and the nozzle plates of aluminum. The optical windows enabled a field of view starting from 9 mm downstream of the throat up to 44 mm downstream of the nozzle exit for flow visualization. On the top nozzle plate, 0.35 mm diameter pressure taps were drilled. At the mid-plane of the plate, 20 pressure taps spaced at 3-mm intervals were drilled, and across the plate, 18 taps 5 mm apart were drilled. An aluminum block with 18 taps along the symmetry line could be installed instead of one of the optical windows. This arrangement enabled measuring the pressure along the top wall and the symmetry plane of the nozzle. The flow could be verified as two-dimensional by measuring the pressure across the top plate.

One of the challenges in 2D flow investigations involves minimizing the 3D effects that result from the sidewalls inside the nozzle and the effect of side flow at the nozzle exit. For this reason the nozzle was constructed with very large width-toheight aspect ratios, which were 32 at the throat and 4 at the exit. Extension of the optical windows 44 mm beyond the exit plane prevented side flow from inducing 3D effects.

An aluminum wedge with a 10° half angle and a width of 100 mm could be inserted and retracted into the nozzle during the test run. The position of the wedge was controlled by a linear stage connected to a stepper motor. The position resolution of the wedge was 0.006 mm. The gap between the wedge and the sidewalls was less than 1 mm, and the deviation of the leading edge of the wedge from the centerline was less than 0.1 mm.

The average pressure was measured with an Omega PX215 pressure transducer (30 psia measuring range, 0.25% F.S. accuracy) connected to a Scanivalve mechanical pressure multiplexer and controlled by a LabView application written for this purpose. The pressure measurement system was calibrated with a Druck model DPI-605 precision calibrator (0.025% of reading accuracy). The sampling procedure was done by reading 500 samples, calculating the standard deviation, and comparing it to a threshold value. When the standard deviation fell below this value, the mean of the 500 samples was calculated and written to a file and the valve was advanced to the next station. In this way, the scanning time was minimal when the pressure exhibited minor change from one station to the next and accurate enough when there was an abrupt change. Far field noise measurements were collected by a B&K model 4939 microphone and recorded at a rate of 44,800 samples/s. The microphone was placed about 1 m downstream from the nozzle exit at 45° off the central axis of the nozzle. An analog device model ADXL204 dual-axis accelerometer was mounted on the back of the aluminum wedge to measure its vibrations. The signal from the accelerometer was recorded simultaneously with the microphone. The stagnation conditions were collected by the LabView application for controlling the Hot Jet Facility at 5-second intervals throughout the duration of the test run. Flow visualization was achieved with a straight line focused shadowgraph system. The light source comprised a high luminosity white LED coupled to a 20-mm FL condenser lens and a rectangular slit. The field lenses were plano-convex with a diameter of 145 mm and 500-mm FL. A 1360x1024 pixel sharpVISION camera was used for recording the images. Frame acquisition control was done by IDT proVISION software with an exposure time of 0.5 ms at 12 fps (see Figure 3). Due to the high humidity in Florida, running the jet at temperatures below ambient conditions led to severe condensation on the optical windows. This was eliminated by flushing the outer side of the windows with warm dry air, although in some flow conditions, minor condensation was seen toward the nozzle exit.

Numerical Modeling

Numerical simulations of flow separation in turbulent supersonic flow regimes are a challenging task. Although the shock reflection process at the symmetry plane is inviscid and poses little numerical problems, the boundary separation process at the wall is much harder to simulate. The standard k-ε turbulence model is inadequate in predicting the separation point because of the adverse pressure gradients at the wall as well as the compressibility effect of the supersonic flow. In a previous study [15] three variants of the two-equation model that are more suitable for supersonic nozzle flows with possible separation were considered: the realizable model, the renormalization group method (RNG) k- ε model, and the shear-stress-transport (SST) k-ω model [18-20]. All three models gave similar results but the RNG k-ε method had a better numerical behavior than the others and thus was selected for the present investigation. Both steady and unsteady Reynolds-averaged Navier-Stokes equations were solved using the commercial finite volume CFD program "FLUENT" using a 2D density based implicit solver, with a second order upwind discretization scheme. The computational domain was constructed with quadrilateral cells whose aspect ratio was close to unity and whose equiangle skew was less than 0.4 in most parts of the domain. To reduce the computation time, the cell area varied according to the zones of interest. The nozzle zone was meshed densely while the jet outside the nozzle and the ambient zone above it were gradually coarsened as the distances downstream of the exit and away from the symmetry line increased. The ambient zone extended approximately 10 and 60 throat heights upstream and downstream of the nozzle exit and 80 throat heights normal to the jet. Early simulations showed that the supersonic jet generated a suction effect, which drew fluid from the top and the right boundaries of the domain, and thus the boundary condition was set to “pressure inlet” instead of “pressure outlet”. In order to capture the asymmetric aspects of the flow the full domain was modeled by mirroring the mesh geometry.

The steady state simulation procedure was carried out in the following order. First, the pressure conditions at the inlet and outlet were set to produce an over-expanded flow with a symmetric separation. The calculation was iterated until the residuals flattened and the mass balance between the inlet and the ambient outlet was within a 2% margin of error. The stagnation pressure at the inlet was decreased by fixed pressure steps until the separation became asymmetric. Then, the pressure was increased at the same increments until returning to the initial conditions. During the whole simulation, the pressure at the outlet of the nozzle was kept constant at 100 kPa. A second set of computations was carried out with the wedge placed at different locations.

A grid convergence study performed in pervious work [15] showed a minor difference in the location of the separation point between the medium and fine grid. It was therefore decided to use the medium grid density for the rest of the simulations. Boundary layer modeling was tested by comparing results using wall functions vs. resolving the mesh down to the viscous sublayer (near wall treatment). In order to account for the pressure gradients near the wall, a pressure-gradient sensitized version of the universal law of the wall was used [21]. Qualitatively the results of both modeling methods were the same with the near wall model predicting flow separation by about 10% of the nozzle length upstream relative to the wall function model.

Experimental Results

The experiments were performed with dry air at nozzle pressure ratios (NPR) ranging from 5 to 15.5. The location of the leading edge of the wedge measured from the throat position ranged from 25 to 125 mm. This distance was used to calculate the crosssection area of the nozzle at the start of the constant area duct generated by the wedge, and from it the area ratio of the nozzle up to the wedge (ARw). The variation of the wedge area ratio was from 3.5 to 8, wedge positions larger than the nozzle length (65.25 mm) were calculated as ARw=8. At each NPR and wedge location, the wall pressure on the top plate was measured and a series of images were taken. At several measuring points, the pressure across the nozzle at X* = 0.3 ( X*=X/XNozzle) was collected to ascertain that the flow was two-dimensional. XNozzle is the distance from the throat to the exit plane of the nozzle. Replacing one of the optical windows with a pressure tap plate enabled recording the pressure along the centerline of the sidewall.

---

---

Flow visualization

Overall, more then 120 measuring points where collected throughout the experiment. The shadowgraph images revealed four different flow patterns as shown in the following figures.

Type "I" flow: When the wedge was inserted deep inside the nozzle, the interaction of the shock from the tip of the wedge with the nozzle walls produced flow separation that started at the lips of the nozzle and proceeded upstream (Figure 4a) as the wedge retracted. Further retraction of the wedge moved the separation point upstream until it was further upstream than the location at which the oblique shock from the tip of the wedge interacted with the nozzle wall. Thus, the wedge shock did not directly produce the separation. The separation shock reflected between the wedge and the jet boundary (Figure 4b).

---

---

The Mach waves that are seen in the images are probably the result of machining direction, which was done by milling the surface in a direction perpendicular to the flow direction. These Mach waves enable measurement of the flow Mach number at different locations along the wall, and these measurements were found to agree with the pressure readings. The images also depict the thickening of the boundary layer along the nozzle wall and the effects of shock-boundary interaction.

Type II flow: From this state, additional retraction of the wedge or reduction of NPR resulted in a substantial instability in the separation location, which was seen as multiple weak shock waves emanating from numerous separation points. The smearing of the shock waves as seen in the shadowgraph could also be the result of highly 3D-flow effects, but this would be manifested in the variation of pressure across the nozzle flow path. Simultaneous with the separation instability a high pitch tone could be clearly detected, and its amplitude and frequency increased as the wedge was pulled out (Figure 5). As NPR increased the transition from type "I" flow took place at larger ARw, and was limited by the maximal pressure the experimental system could supply.

---

---

Type III flow: Further retraction of the wedge caused the screechlike sound to stop, and the flow stabilized with the separation shock converging at the leading edge of the wedge. The oblique shock from the wedge interacted with the jet boundary from the separation point causing it to bend outwards and accelerate the flow. The noticeable reduction in the boundary layer size downstream of the separation shock suggested that a reverse flow was taking place as in rocket nozzles with Free-Shock-Separation (Figure 6a). For NPR greater than 15, this flow pattern remained basically unchanged when the wedge was completely retracted from the nozzle (Figure 6b). The separation shock from each of the walls reflected at the symmetry plane with a regular reflection.

---

---

Type IV flow: For NPR values below 15, further increase in the area ratio at constant NPR by retraction of the wedge caused the flow to separate asymmetrically with the jet reattached to either the top or the bottom walls of the nozzle (Figure 7). The reattachment of the jet to the wall resembled RSS with a closed circulation bubble while the opposite side resembled FSS with reverse flow. The flow reversal was noticed when ingress of humid air from the chamber caused the windows to fog up. In most cases the direction of the asymmetry remained constant during the same run but could change direction if the nozzle alignment was changed between runs. The separation point on the flow reversal side moved upstream while on the flow side it remained almost unchanged. This flow pattern remained constant even when the wedge was fully retracted.

---

---

Pressure measurements

The pressure measured across the width of the nozzle at X* = 0.3 is shown in and Figure 8. It reveals that the flow remained two dimensional at all NPRs and wedge locations. The value of ρ/ρ0 = 0.05 corresponded to a flow Mach number of 2.6 as expected from the pressure-Mach number relationship at this area ratio. In the case of NPR = 5.8 and ARw= 8, the separation was upstream of the measurement points, and therefore, the pressure ratio was higher.

---

---

Pressure measurements were taken along the mid-section of the top nozzle wall from X*=0.06 to X*=0.93. The separation Mach number just upstream of the separation point calculated from the pressure readings ranged from 2.6 to 3.0 according to the NPR. Based on the flow patterns that are revealed by flow visualization, a plot of the static wall pressure is presented for each of the flow types. The pressure is normalized by the ambient pressure. Each set of points is the result of a pair of NPR and wedge position values. For a steady flow with a separation point downstream of the leading edge of the wedge, the decline in the pressure upstream of the point of separation closely followed isentropic relation (1):

The pressure increase across the separation point intensified as NPR increased because the separation was at a higher Mach number. The pressure recovery downstream of the separation point was almost linear, ending at 80% of the ambient pressure (Figure 9a). Once the flow separation became unstable, the pressure rise across the separation point was less distinctive, probably due to an averaging effect. For NPR < 8, the normalized pressure downstream of the separation point was about 0.5 and for NPR > 8 it was about 0.6 and remained steady, increasing gradually toward the nozzle exit (Figure 9b). When the flow restabilized, the sharp increase in the pressure across the separation point could be seen once again, but the pressure recovery was immediate, and the pressure remained constant until the nozzle exit. When the leading edge of the wedge was outside of the nozzle (X*w > 1), the pressure recovery was about 90% of the ambient pressure, but when the leading edge of the wedge was inside the nozzle the pressure was lower and it depended on the wedge location (Figure 10a).

---

---

For the case of asymmetric separation, the pressure profile was different for each wall, along the wall that the flow was attached to the pressure increased to about twice the separation pressure down to the point at which the flow reattached to the wall causing the pressure to increase above the ambient pressure. As the NPR increased, the reattachment point moved downstream toward the nozzle exit. On the opposite wall the pressure downstream of the separation point rose immediately to the ambient pressure and remained constant until the nozzle exit (Figure 10b).

The pressure was also measured on the sidewall of the nozzle along the symmetry line from X*=0.2 to X*= 0.9. In general, the pressure at the same X* location was equal for the wall and the symmetry line upstream of the separation point. These findings that are in agreement with analytical and numerical calculations imply that in a conical nozzle the Mach numbers at the centerline and at the wall are almost the same. Pressures measured downstream of the separation point or the leading edge of the wedge were more complicated to interpret as 3D-effects became significant.

---

---

Sound and vibration measurements

Far field sound measurements with a microphone positioned at 45° to the jet axis were taken at various NPRs and wedge locations. In the cases where the flow separation was steady no distinct frequency was found, and the noise was broadband in nature. Once the instability of the separation point location was observed, a loud, high-frequency tone was recorded. FFT of the signal showed discrete peaks with a fundamental frequency of 1200 to 2000 Hz with two to three harmonics. Once the flow re-stabilized with either a symmetric or asymmetric separation, the sharp tones vanished. Figure 11 shows one example of the evolution of the tone at NPR=10.2 while the wedge was retracted from the nozzle to create different flow types. It appeared that the noise generation was directly related to the instability of the separation point location. In general, the fundamental frequency of the tone ascended as the distance of the leading edge of the wedge from the nozzle throat increased. For a constant wedge location, the frequency ascended as the NPR increased. This observation is further analyzed in section B of the numerical results and discussed in chapter VI.

---

---

The vibration of the wedge was measured with a miniature accelerometer attached to the back of the wedge. The natural frequency of the wedge was measured by exciting it mechanically with no flow. The basic frequency measured was between 120 to 200 Hz with harmonics up to 2200 Hz. When the flow was on, the dominant frequencies of the wedge at all positions were around 1200 Hz and 5500 Hz, these frequencies remained mostly unchanged whether the tone was produced or not. In the cases the nozzle produced a tone; its fundamental frequency could be detected by the wedge accelerometer (Figure 12).

---

---

Numerical Results

Simulation of flow without wedge

In previous simulations by Shimshi [22] only half of the nozzle was modeled and a symmetry boundary condition was imposed at the symmetry plane. This prevented the detection of asymmetric effects in the flow domain. To account for such effects, the top part of the domain was mirrored so that the full domain was modeled but asymmetric effects could not be attributed to grid irregularities. The steady state simulation was carried out in a manner similar to that presented in [15]. Mach number contours showing symmetric separation in a tapered nozzle without a wedge are presented in Figure 13a. For this case of separation, a classic RR flow pattern was observed. The jet boundary from the separation point interacted with the reflected shock and diverted the flow toward the nozzle wall, resulting in a wavy pattern that formed shock cells. The jet maintained its integrity for a long distance showing signs of Kelvin-Helmholtz instability near the end of the computational domain.

The wall and the centerline pressure measurements were in good agreement with the numerical simulation. The discrepancy in the centerline pressure at X*=0.75 suggested that the separation was not precisely symmetric (see Figure 13b). This could be exemplified by the results shown in Figure 14 for an NPR=13 simulation. The figure shows a pressure rise on both the top and bottom walls of the nozzle at different locations. The centerline pressure decreased to the point at which it crossed the oblique shock that emanated from the bottom separation point. From this point, the pressure rose gradually until the reflected shock was crossed and then increased rapidly until the point at which the reflected shock interacted with the jet boundary. The expansion fan downstream of this point reduced the pressure and accelerated the flow.

---

---

---

---

For the case of asymmetric separation (Figure 15), the jet was attached to one of the walls, and the separation point on its side was further upstream than that on the opposite wall. The interaction of the oblique shocks coming from the opposing walls was an RR, as in the symmetric case. The shock cell pattern was also maintained, with the cell decreasing in size as the jet dissipated. The absence of jet boundary instability in this simulation could be due to the coarser grid away from the jet center.

---

---

A comparison of the wall pressure measurements at NPR = 6 to the results of the simulation shows good agreement (see Figure 16). The location of the separation point was accurately predicted as were the two large peaks in the pressure at X*=0.6 and 0.9, although the simulation predicted them slightly downstream of the measured locations. The absence in the measurements of the two small peaks and the valley between the large peaks could be due to the smearing caused by jet instability.

---

---

The shadowgraph images (see Figures 5-7) show Mach waves emanating from the walls of the nozzle as a result of some surface roughness. This roughness is known to affect the boundary layer and, therefore, the location of the separation point. This possibly explains the downstream shift of the experimental curve compared to the numerical results that can be seen in Figure 16. To investigate the effect of surface roughness on the separation process, five levels of roughness ranging from 1 to 100 μm were simulated by using the law-of-the-wall modified for roughness. The roughness increased the velocity defect and skin friction and shifted the velocity law of the wall plot downward. For sand grain roughness, the velocity shift for high speed flow collapsed to the incompressible correlation when van Driest II scaling wasused [23]. The thickness of the boundary layer upstream of the separation point, at X*=0.3, increased from 0.54 mm to 0.76 mm with the increase of the surface roughness parameter from 1 to 50 μm. As a result, the separation point moved upstream from X*sep = 0.5 to X* sep = 0.35. Measuring the thickness of the boundary layer from the shadowgraphs at NPR=10.2 and X*=0.3 gave values of 0.5-0.6 mm.

A simulation was conducted to investigate the transition from asymmetric to symmetric separation. The simulation was initiated at NPR=11, where the separation was asymmetric, and in each calculation the NPR was increased by ΔNPR=0.5 until the separation became symmetric. Figure 17 and Figure 18 show that the attachment of the jet to the nozzle wall generated a closed circulation zone that was characterized by flow reversal at the wall and static pressures below ambient conditions. This low pressure region drove the separation point toward the nozzle exit while on the opposite side the pressure was equal to the ambient and the separation point was further upstream. Downstream of the circulation bubble, a high pressure region was located on the wall where the expansion fan from the interaction of the reflected shock and the jet boundary interacted with the wall. This high pressure region prevented fluid from the surroundings to enter the circulation bubble. As the NPR was increased, the separation points and the whole shock system moved upstream until the high pressure region was pushed out of the nozzle. This opened the path for fluid from the surroundings to enter the circulation region, thus increasing the local pressure and pushing the separation point on the top wall back upstream.

Figure 18 shows that a circulation region also exists on the bottom wall toward the nozzle exit, but this open circulation bubble did not lower the static pressure as on the top wall, and thus, it did not affect the location of the separation point on the bottom wall. The shadowgraph images show that the transition from asymmetric to symmetric separation took place at an NPR value higher than 13.6 compared to 13.0 in the simulation.

---

---

---

---

Another set of simulations was conducted to test whether a hysteresis effect existed in the transition from symmetric to asymmetric separation and back. The simulation was conducted in a similar method to that described previously with ΔNPR=0.05. After the transition from asymmetric to symmetric separation, the NPR was decreased in the same manner until asymmetric separation occurred again. Figure 19 shows the location of the separation point on the top and bottom walls as a function of NPR on pressure increase and decrease where the hysteresis loop can be clearly seen on the top wall. The experimental findings also supported the existence of such a phenomenon, but on a much smaller scale of pressure ratios. It is assumed that the transition to asymmetric separation is triggered by flow instability, as shown in the observations of the flow with a wedge inserted into the nozzle.

---

---

The finding that the transition from asymmetric to symmetric separation on the top wall had no effect on the location of the separation point on the bottom wall was a surprise. This supports the assumption that the location of the separation point on each wall is determined solely by the pressure downstream of its separation point. On the attachment side, the pressure ratio across the separation point is affected by the change of the jet attachment. On the opposite side, the pressure downstream of the separation point remains constant during the shift form asymmetric to symmetric separation.

Steady and unsteady simulations of flow with a wedge

The steady state flow with the wedge was simulated by adding its contours as solid walls to the calculation domain. For each wedge location, a separate domain was built and meshed to maintain good quality cells. As can be seen in Figure 20, the simulation replicated the experimental results in cases where the separation location was steady (flow Types I, III and IV).

---

---

The predictions of the general flow features, such as the locations of the shock waves, the location of the separation points and the shape of the jet boundary, were accurate. Good agreement was achieved in comparing the pressure along the wall of the nozzle up to the point of separation. However, it was not possible to compare the simulation to the experiments for the type II flow since it was, in principle, unsteady.

The shadowgraph images showed that under certain stagnation conditions and wedge locations, the separation point could appear either in a constant location or in varying positions. Unsteady simulations were performed in an effort to replicate this phenomenon. Initially, a steady state calculation with NPR=10.35 and the leading edge of the wedge located at ARw = 4.09 was iterated until convergence was achieved. Then the solver was switched to transient mode with second-order time marching and 50-μs time steps. The calculation ran for about 1000 time steps, and the points of separation on the top and bottom walls were calculated at each time step by finding the cell adjacent to the wall where the x-velocity component dropped below zero (point of flow reversal). This procedure was repeated for the same NPR and, and after 2.5 ms the time step was reduced to 5-μs to test whether it influenced the results. At ARw = 4.09 the fluctuation in the location of the separation point was minimal and appeared to decrease with time, while at ARw = 4.64 it increased with time until it spanned 30% of the nozzle length (see Figure 21). The oscillation was sinusoidal in nature with a frequency of about 1000 Hz. In the latter case (ARw = 4.64) the separation was symmetric with the separation point precisely at the same location on the top and the bottom walls, but in the first case it seemed to be antisymmetric, that is, moving in equal but opposite directions.

---

---

To ascertain that this result was not a numerical artifact, three alterations to the model were performed. The calculation domain outside the nozzle was increased in all directions by 50%, the number of cells outside the nozzle was quadrupled, and the “pressure inlet” boundary condition was replaced by a "far field" pressure condition. None of these modifications changed the oscillation of the separation point and had only a small influence on the frequency and amplitude.

A second set of simulations was performed at a constant location of the wedge (ARw=4.64) and at decreasing stagnation pressures. Each simulation ran for 1000 time steps at 5 μs. The average and the standard deviation of the separation point location were calculated (see Figure 22 and Figure 23). At NPR > 12.4, the flow was steady with no flow separation or with a local separation caused by the interaction of the oblique shock from the wedge with the boundary layer on the wall. The location of this separation point was not affected by the changing stagnation conditions. A second separation point due to the adverse pressure gradients that moved upstream as the NPR decreased was downstream of the first. Below NPR=11.9, the separation due to the pressure gradients was upstream of the interaction between the oblique shock and the wall, and its location became unstable. For 11.9 > NPR > 9, the oscillation was sinusoidal and anti-symmetric (the separation points moved in opposite directions on the top and the bottom walls). The amplitude of the oscillation was constant at a frequency of 1400 Hz. Below NPR=9 the oscillation became symmetric, the amplitude of the oscillation decreased with NPR, and the frequency dropped from 1300 Hz at NPR=9.0 to 890 Hz at NPR=6.9. At NPR=6.5, the frequency jumped to 2900 Hz with a very small amplitude, and at a lower stagnation pressure the separation was asymmetric and stable.

---

---

---

The location of the separation point was calculated as the mean of the temporal separation locations, and the amplitude was taken as the standard deviation of the fluctuations. For comparison, the separation point location at ARw = 4.64 from the experiment was estimated by interpolating between the locations of the two pressure taps just upstream and downstream of the location where an increase in the pressure along the wall of the nozzle took place. The error in this method of estimation was assumed to be half the distance between the two pressure taps.

Symmetric and anti-symmetric modes were reported by [24] for a choked planar nozzle that depended on the nozzle pressure ratio.

At low NPRs, the mode was symmetric with its frequency strongly dependent on the pressure ratio, while at high NPRs, the mode was anti-symmetric with a small dependency on the frequency.

The pressure along the wall at the nozzle exit plane and just downstream of the separation point was recorded at each time step. An FFT analysis showed a dominant frequency at 1470 ± 200 Hz with several harmonics of decreasing amplitude, the peak noise level was 170 dB SPL. The sound pressure level 300 mm and 45° from the nozzle outlet decreased to 140 dB SPL. Judging by the sequence of pressure contours, the source of the disturbance was at X*=1.25 and generated a concentric pressure fluctuation that traveled to the nozzle outlet (see Figure 24).

---

---

---

This generated a cyclic mechanism in which the pressure downstream of the separation point decreased, thereby pulling the separation point downstream. At some point this pressure was significantly lower than the outlet pressure and it began to rise. This pushed the separation point upstream until the pressure was close to the outlet pressure, then the process reversed.

Discussion

Asymmetric Separation

Both experiments and numerical simulation revealed symmetric and asymmetric separation depending on the NPR. At NPR < 14 asymmetric separation depended on the nozzle AR determined by the wedge, at higher NPR values the separation remained symmetric up to the maximal AR. The numerical simulation suggests a mechanism for this phenomenon. The location of flow separation on both walls of the nozzle is susceptible to changes in the pressure downstream of the separation point. The free jet outside the nozzle creates fluctuations in the pressure at the lips of the nozzle, and as the pressure is lowered on one side of the jet the separation point moves upstream and the jet bends towards that side (as seen in Figure. 14). If the curvature of the jet boundary, caused by the RR, creates a narrow passage to the nozzle wall the reverse flow velocity near the wall increases and the static pressure on that side of the jet reduces. This creates a positive feedback mechanism that pushes the jet towards the wall until attachment occurs. This attachment is similar to RSS while on the opposite side of the jet it is similar to FSS. Previous experiments with planar nozzles did not show this type of asymmetric separation as the Mach number of the jet was lower than 2.2 and resulted in an MR instead of an RR, which creates a straight jet.

The high pressure region at the wall where the expansion fan from the interaction of the reflected shock and the jet boundary interacted with the wall prevented ambient air from entering the closed circulation bubble and maintained a low pressure region just upstream of the separation point (as seen in Figure. 18). Only when the NPR was raised high enough to clear a path for the ambient air the pressure on the attached side of the nozzle increased to push the jet back to its symmetric position (Figure. 19). The proposed physical mechanism could not be verified by the experimental setup as it was not fitted with dynamic pressure measurements. This mechanism does explain why there is a hysteresis in the transition from symmetric to asymmetric separation, which has been observed in the experiment.

Unsteady separation

Both the experiments and the numerical simulations revealed instability in the location of the separation point at certain conditions. There were three possible sources for this instability: upstream fluctuations, vibration of the wedge, and downstream acoustic reflections. An attempt to elucidate which of these three sources can be responsible for this instability is presented subsequently.

The air inlet supply system had control valves and other mechanical elements that could induce fluctuations in the air stream and promote the instability of the separation point. But as the experiment was held under constant stagnation conditions for a series of wedge position locations, it alone could not explain the distinct regions of stability and instability that were encountered.

The wedge was connected to the linear slide with two rods, and thus had some flexibility and could be self excited by the flow. The oscillations generated by the movement of the wedge were expected to be at the natural system frequencies [25]. The natural frequency of the wedge was measured by fitting it with an accelerometer and exciting it mechanically. The basic measured frequency was 160 Hz with harmonics up to 2200 Hz. When self excitation occurs, the lowest frequencies are usually those that react the most. If the instability of the separation point was due to the vibration of the wedge, it would be expected that the frequencies would be in the same order of the lowest mode. Furthermore, stiffening the rods connecting the wedge to the slide in order to change the natural frequency did not affect the tone emitted by the nozzle.

Three mechanisms that could produce discrete tones due to flow are edge tone, screech, and acoustic resonance. Holger et al. [26] claimed that an edge tone could develop in a planar jet flow with a wedge if there is a periodic disturbance at the jet origin.

The vortex street propagates from the jet origin to the leading edge of the wedge, and a feedback mechanism strengthens the intensity of the waves to produce the high intensity tone. The fundamental frequency is governed by the standoff distance between the nozzle exit and the leading edge of the wedge, and the exit flow velocity. It exhibits discrete jumps (modes or stages) as the parameters are changed up to sonic velocities [27]. Thus the frequency drops as the distance from the source of the flow to the sharp edge increases and jumps up when the mode advances. For a fixed standoff distance the frequency increases linearly as the jet velocity increases. In our case the distance from the throat to the leading edge of the wedge can be regarded as the stand off distance and the NPR relates to the jet velocity. While the frequency did increase with NPR it did not decrease with standoff distance and no staging behavior was detected.

Screech, on the other hand, is produced in a supersonic jet, which has a shock cell pattern (as seen in Figure 13a). In this case, the feedback mechanism is between the cell structure and the nozzle lips. Screech is a complex phenomenon that involves at least four processes: instability wave growth, instability shock-interaction, acoustic feedback, and receptivity process [28]. Although it has been studied for more the 50 years, screech is not completely understood. The screech frequency, f , is related to the convective speed of the hydrodynamic disturbance, UC, by the relation:

here s is the shock cell spacing, and MC is the convective Mach number, Ui . ci are the velocity and speed of sound in and out of the jet. In the case of a jet flowing into stagnant air Uc ≈ 0.5U1 s ≈ 10 ÷ 20mm and the resulting screech frequency should be above 5000 Hz. Further more, as the NPR increases, the screech frequency should decrease. In the present experiment the frequency increased with increasing NPR, which does not fit the observed phenomenon. Raman noted that the source of the screech was in the third or fourth shock cell, depending on the fully expanded nozzle Mach number, and it had an asymmetric mode. The numerical simulation showed that the source of the pressure fluctuations was between the second and third shock cell depending on the NPR but had both symmetric and asymmetric modes. Lin & Powell [24] who investigated a rectangular choked nozzle with a wedge in front of it, reported that when the wedgewas close to the nozzle, an edge tone was produced, and as the wedge was moved further away from the nozzle, the edge tone transitioned to choked-jet screech alone.

Zaman et al. [30] described a loud tone produced from a CD nozzle when a shock existed within the diverging section of the nozzle. This tone was found in several nozzles types, including planar nozzles, and it was named ‘transonic resonance’ because the fully expanded Mach number (Mjet) calculated from the isentropic relation of the stagnation pressure was in the range 0.4-1.6. The nozzles investigated in Zaman's work had area ratios of 1.1-2.8, divergence angels of 1.3-8.3°, and an NPR range of 1.2-4. Table 2 compares the properties of transonic resonance to those found in the present study. Some of the features highly resemble each other. While certain differences could be related to the different operation conditions, others cannot be explained.

---

---

The underlying mechanism of the transonic resonance is similar to that of acoustic resonance in a duct, which has one end open and the other closed (the closed end being the throat of the nozzle). In this type of duct, only odd harmonics of the fundamental frequency are possible. On this basis, Zaman developed an expression to predict the frequency as a function of the nozzle geometry and the operating pressure. Applying this expression to our case is not straightforward, as the nozzle length in Zaman’s expression has to be modified to reflect the distance from the separation shock location either to the nozzle exit or to the tip of the wedge. It is not clear if the length of the constant area duct (from the leading edge of the wedge to the nozzle exit) has an influence on the frequency. The fact that no staging behavior has been found in the present experiment or that both odd and even harmonics are detected seems to rule out the assumption of a standing 1/4-wave. The unsteadiness of the separation shock seems to act as a vibrating diaphragm that promotes the acoustic tone.

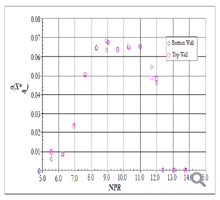
Frequency scaling of the data can be done by using the Strouhal number S = fL/U. The numerical simulation showed direct relation between the pressure fluctuation at the outlet of the nozzle and the location of the separation point, therefore the length of the constant area duct was chosen as the length parameter. This claim is supported by Wong [33] who overviewed flow separation in transonic and supersonic flows and concluded that the resonant frequency depends on the distance between the separation shock and the downstream pressure fluctuation outside the nozzle. Figure 25. shows the dependence of the NPR on the screech Strouhal number, S = fLexit/Uexit , where Lexit is the length from the leading edge of the wedge to the nozzle exit plane. The exit velocity is calculated from Uexit = m. ρamb Aexit . A good collapse of all the data was achieved. This was not the case when using the distance from the throat to the wedge as a length parameter. A nearly linear decrease of the Strouhal number with the increased NPR is evident for all wedge area ratios. Mjet is the fully expanded jet Mach number for the corresponding NPR.

---

---

---

It is therefore proposed that the mechanism producing this tone is a combination of screech and acoustic resonance. When the wedge is inserted into the nozzle, the shock cell structure is split by the wedge into an upper and a lower surface and follows its inclination. As it moves in and out of the nozzle or as the NPR is changed, the location and the shock cell spacing adjust to the flow condition in a non-simple manner. The simulation shows that for equal NPRs, the shock cell spacing with the wedge is smaller than the shock cell spacing without a wedge, and only 2-3 shock cells are visible. Transient simulations show that strong pressure perturbations are emitted between the second and third cells. These pressure fluctuations advance upstream in the separated region up to the separation point and generate a feedback mechanism that locks the frequency emitting the discrete tone. The separation point is susceptible to the variation in the pressure at the exit plane and thus its location varies accordingly. The lower limit of this condition is when the separation point is downstream of the shock-boundary-layer-interaction from the oblique shock formed by the leading edge of the wedge. The gradual decrease in the amplitude as the wedge is retracted (or as the NPR is decreased) is not clear but seems to be related to the transition from an anti-symmetric to a symmetric mode.

Conclusions

An apparatus for investigating flow separation phenomenon inside CD planar nozzles has been devised. It enables examination of the effects of continues change in area ratio on the mechanics and dynamics of flow separation at constant stagnation conditions by changing the location of the leading edge of the wedge. Alternately it enables measuring the effects of variable NPR conditions at different positions of the wedge. The numerical simulations showed good agreement with the experimental findings and reproduced all the major flow features.

Flow visualization revealed four types of flow patterns depending upon the NPR and the wedge position. Three of the flow types resulted in a steady flow either without flow separation or with symmetric or asymmetric flow separations. The forth produced an unstable separation mechanism that was accompanied by a distinct tone. Stable symmetric separation without the wedge could only be achieved at NPR > 14, which was higher than those reported by [4] and [3].

The separation Mach number ranged from 2.6 to 3.0 and produced a regular reflection, RR, with a typical shock cell formation and a wavy jet boundary for all cases. The attachment of the jet to the wall was triggered by flow instability that moved the jet out of the symmetry plane. As a result, the pressure in the separated region on that side was lowered thus exerting a greater force on the jet towards the wall until attachment. The wavy form of the jet boundary caused by the RR interacted with the wall to generate a high pressure zone upstream of the separation bubble. Only when this high pressure zone was pushed out of the nozzle, could the jet detach from the wall and resume symmetric separation. In previous experiments where the separation Mach number was lower than about 2.2, a Mach reflection, MR, flow pattern was formed with a relatively straight jet boundary, and this prevented the attachment of the jet to the wall and led to a Lambda foot formation. The transition between symmetric and asymmetric flow separation exhibited a hysteresis effect in which the NPR required to revert from asymmetric to symmetric separation was higher than that required to trigger it.

The unsteadiness of the separation point location observed in the experiment and in the numerical simulations was related to a form of jet screech. The shock cells that were formed on the surface of the wedge outside the nozzle emitted some pressure disturbances due to flow instability. These pressure disturbances propagated upstream to the nozzle exit plane and affected the location of the separation point and in turn both the reflection point and the shock cells were affected. This intensified the disturbance emitted from the shock cells and the process was maintained.

At a high enough NPR the location of the separation point was upstream of the interaction point of the oblique shock from the wedge with the wall. This prevented the pressure fluctuations from changing the separation point and thus the feedback mechanism was broken. At low NPRs the amplitude of the oscillation decreased and the mode changed form anti-symmetric to symmetric. The reason for this is yet to be determined.

Acknowledgments

The first author would like to thank Prof. Krothapalli for hosting him at Florida State University, without his help this work would have not been possible. To Dr. Alvi and Dr. Kumar, for helping in performing the experiments at their Advanced Aero-Propulsion Laboratory. Especially, I would like to thank Dr. Brent Greska for his help and advice on the work done in the Hot Jet Facility.