Keywords

Thalassemia Disease; Pure Fraction; Reducible Pure Fraction; Mathematical Model; Monte Carlo Simulation; MATLAB.

Introduction

Thalassemia disease: An Overview in the recent few decades, Thalassemia has recently become a serious threaten and spread widely worldwide. "Thalassemia", a Greek word that means the Mediterranean basin or Cooley's anemia, it is a form of inherited blood disorder in which the body makes an abnormal from of hemoglobin [1, 2]. It is most widespread between people of Middle Eastern countries, Greek, Italian, South Asian, and African descent [1]. Hemoglobinor (Hemoglobin) is the protein molecule in red blood cells which contains iron. It is used that carries oxygen around the human body [3]. The disorder results in excessive destruction of red blood cells, which leads to anemia; anemia is a condition in which your body doesn’t have enough normal, healthy red blood cells [4].

Thalassemias are genetic disorders inherited from a person's parents [1]. This means that one of the parents carries thalassemia that caused by missing genes which produce the hemoglobin in the human body. If both parents are carriers of thalassemia, the probability of inheriting a more serious form of the disease is greater. The destruction of red blood cells and inappropriate of oxygen transporters leads to forming the abnormal hemoglobin in the body [5].

Persons with thalassemia disease have a fewer red cells blood and less hemoglobin comparing with not infected persons. From moderate to severe anemia, thalassemia kind depends on the physiological conditions of the body. There are two main types, Alpha-thalassemia (α-thalassemia,) and Beta-thalassemia (β - thalassemia) [1], with three types Beta-Thalassemias major (no Alpha-globin assembled), intermediate (some of Alpha-globin is produced) and finally minor (one of the two Beta-globin has a mutation) [6]. The common complaints and signs can be resulted from thalassemia may include Complications may include bones deformity, iron overload and cardiovascular illness. Thalassemia makes the bones marrow expand, thin, brittle and increasing the risk of broken bones, especially in the face and skull areas [6].

The present work introduces a simple and effective methodology for Thalassemia based on the theory of the pure fractions. The developed methodology is suitable for application in a much wider range of thalassemia disease. We define the concept of pure fractions relevant to the considered genetic diseases (Thalassemia). In this paper, we use pure fractions to create a mathematical model for controlling thalassemia disease diagnosis and how to perform Monte Carlo Simulation in MATLAB.

The rest of the paper is organized as follows: in Section 2, Preliminaries - mathematical background was introduced. Section 3, presents pure fractions and thalassemia disease. We create a mathematical model for thalassemia disease in section 5, while, an applicable example was explained in section 6. Monte-Carlo Simulation model was built and explained in section 7; also results, discussion and conclusion of the mathematical model are given in Sections 8 and 9 respectively.

Preliminaries - Mathematical Background

Theory of numbers is the fundamental theory of mathematics. In the past, this theory has concentrated essentially on the properties of integers [7]. However, in recent times, the theories and properties of other classes of numbers have proved worthy of more formal investigation [8]. Among the class of numbers whose theory attracts much attention are the numbers in the unitinterval (UI) [0, 1], which we call pure fractions [7].

In mathematics, fuzzy sets are sets whose elements have degrees of membership. Fuzzy sets were introduced by Lotfi A. Zadeh and Dieter Klaua in 1965 as an extension of the classical notion of set [9, 10]. At the same time, Salii, defined a more generic type of structure called an L-relation which is applied in an abstract algebraic context [11].

Fuzzy relations are special cases of L-relations when L is the Unit -Interval (UI) [0, 1] Figure (1). The UI is the closed interval [0, 1], that is, the set of all real numbers (R) that is greater than or equal to 0 and less than or equal to 1 (≥ 0 and ≤ 1). It is often denoted by I [12, 13]. In the literature, the term "unit interval" is sometimes applied to the other shapes that an interval from 0 to 1 could take: [0, 1], [0, 1], and [0, 1].

---

---

In this paper we formalize some properties of pure fractions and give a biologically related application. We shall create a new form of representation for a given pure fraction. The motivation for the new form is the nature of the numbers 0, 1/2, 2/3, 3/4, 4/5... Which are numbers expressible in the form ( 1-1/n) for an integer n ≥ 1. We call such numbers co-harmonic fractions. An important characterization of a pure fraction s is that s can be represented in definition (4:1) – section 4. These preliminaries and concepts will be addressed in subsequent items of the research.

Pure Fractions and Thalassemia Disease

The current work presents an efficient and simple methodology for thalassemia transition based on the theory of the pure fractions. This developed methodology is proper for implementation in a much wider domain of thalassemia and other genetic diseases. Through that methodology, the concept of pure fractions relevant to the genetic disease (thalassemia) was defined. In this section, a mathematical model is developed to handle the diffusion of the thalassemia gene in which the concept of reducibility of pure fractions is utilized. The concepts such as reducibility, representation of pure fractions and the fuzzy sets has a significant role in the development of the mathematical model of the current study.

Consider a hypothetical genetic disease (d) and a gene (g) responsible for the disease. We imagine that every number in the unit interval [0, 1] as representing a possible genotype for g. That is, each pure fraction s ∈ [0, 1] measures a corresponding degree of possession and transmission of the gene g by an individual denoted by X, as done in fuzzy logic for truth values Nguyen and Walker [14]. It is noticed here that the pure fraction can also be thought of as the probability of possession and transmission of the gene g by the individual denoted by X [13]. A person with a “high incidence” of the gene g is defined as someone who has a genotype falling in the sub-interval I2 = [1/2, 1].

An individual with such genotype may suffer from discrimination when selecting a spouse. However, we make the proposition that such an individual would like to have a spouse so that their descendant of some future generation would be more providential and would have a genotype of g that does not fall in sub- interval I2. Such an individual is a descendant with a “low incidence” of g and has a genotype that falls in the subinterval I1 = [0, 1/2]. Based on what is stated above, we will devise a mathematical model, where an individual with a high incidence of the gene g can be matched with the appropriate spouse so that a future descendant can have a low incidence of the gene g.

Reducibility of Pure Fractions Representation

The theory of pure fraction originates from the work on the application of fuzzy sets [13]. In this section we will introduce some known and useful definitions; propositions; theorems; regarding pure fractions which will be used for creating the mathematical model to control the transmission of thalassemia disease.

Definition(4:1)

If s is called a pure fraction defined on the UI [0, 1], then s can be represented in the following forms:

s= (r+ α-1)/α, Where: r ∈ [0 ,1], and α is a positive real number. Let R+ be the set of non-negative real numbers (R), then for a given pure fraction and a positive real number α, we define r[α] by: r[α] = (r + α-1)/α, (i.e. every pure fraction can be represented in the above form, if r[α]∉ [0, 1] then it is called indeterminate).

Definition (4.2)

Reducibility of the pure fractions is generated by the two subintervals of [0, 1], i.e., irreducible pure fractions are defined in the subinterval [0 , 1/2] and reducible pure fractions are defined in the subinterval [1/2, 1].

Definition(4:3)

Two sequences {xn} and {yn} of pure fractions are said to constitute a Genetic Remediation Scheme (GRS) if:

1) x1 is reducible
2) yn = xn[1/2] = 2 xn - 1, n = 1,2,…
3)x(n+1) = 1/2 (xn+yn)
4) The iteration stops when xN is irreducible for some positive integer N.

Theorem (4:4)

The sequences {xn} and {yn} of pure fractions that constitute a Genetic Remediation Scheme (GRS) are decreasing and finite. Furthermore, for every k such that {yk} is reducible we have:

y(k+1) ≥ yn[1/2].

Proof: first we want to prove that the sequences are decreasing and reducible. It is given that there are two sequences {xn} and {yn} with a GRS property, definition (4.3), then we have {yk} such that:

yk = xk[1/2] = 2 xk - 1 < 2 xk - xk = xk, xk[1/2] = 2 xk - 1,

this implies that:

x(k+1) = 1/2 (xk + yk) < xk, then y(k+1) = x(k+1)[1/2] < x(k)[1/2] = yk.

In addition we have: yk < xk → y(k) < 1/2 (xk + yk) = x(k+1).

Hence, y(k)[1/2] < x(k+1)[1/2] whenever yk is reducible.

Second to prove the sequences are finite, suppose there exists no positive integer N s.t xN is irreducible.

Then xn ≥ 1/2, ∀n. Since {xn} is decreasing and bounded, {xn} converges to some pure fraction s. Similarly, {yn} converges to some pure fraction t. Consequently,

s = limn →∞ x(n+1) = 1/2 limn→∞(xn + yn) = 1/2 (s+t). Thus s = t.

Then,

s = limn→∞ yn = limn→∞(2xn - 1) = 2s - 1 → s = 1 But s ≤ x1 ≤ 1. Therefore, we have a contradiction and this completes the proof.

Proposition 4:5

Let s ∈ [0, 1]. Then, the following conditions are equivalent for a positive integer n.

1. s = r[n] For some r ∈ [0, 1]
2. i (s, 0) ≥ n
3. 1 > s ≥ 1 - 1/n.

Definition 4:6

A pure fraction s is called reducible if s satisfies any of the equivalent conditions of Proposition 4:5 for some integer n ≥ 2. Otherwise, s is called irreducible. As a consequence of Proposition 4:5, a pure fraction s is irreducible ↔ s = 1 or s < 1⁄2. Thus, we have a partition of [0, 1] into I1 = [0 , 1/2] & I2 = [ 1/2 , 1] consisting, respectively of irreducible and reducible pure fractions. Based on the above definition, we have a partition of the UI [0, 1] into: I1 = [0, 1/2], and I2 = [1/2, 1] to determine the reducibility and irreducibility of the pure function which controls the transmission of the thalassemia as follows:

S = I1 = [0, 1/2], irreducable pure fraction ( keep iteration)
       I2 = [1/2, 1], reducable pure fraction (stop iteration)

Mathematical Model for Thalassemia Disease

The mathematical model was developed based on the definitions, theories, and assumptions that have been mentioned in sections 3 and 4. Also, we adopt previous studies uses a mathematical model for the control of the transmission of genetic diseases using pure fractions conducted by Boniface Eke1, Asamoah Nkwanta; and S. Thakur et al; 2016 [13, 15]. The theory and properties of pure fractions are used which are defined by Eke in 2008 [13].

Suppose that g denotes a gene which is responsible for the Thalassemia disease T. Also, there is a function:T: H → [0, 1], s.t the following assumptions are satisfied:

For a “genotype” t = T (X) the followings are holds:

X is completely free of g ↔ t = 0
X has a “low incidence” of g ↔t ∈ [ 0 ,1/2]
X has a “high incidence” of g ↔t ∈ [ 0 ,1/2]

If t = rn, then r is also in the range of T.
The genetic structure of an individual is proportional to that of his/her parents x', and y', hence:

T(x) = 1/2 [(T(x') + T(y')]

If both T(x') and T(y') are in danger of the Thalassemia disease T then an individual Y will not accept X for a marital partner if:

T(y) < min (T(x')[1/2] +T(y')[1/2])

Since we have the function T : H →[0, 1], then we can set the condition “marital connections” such that an individual X with genotype T(X) ∈ [0,1] can be “tolerated for marriage” by an individual Y only if they can have a descendant Z, such that T (Z) ∈ [ 0, 1/2]. Now to solve the problem “marital connections” suppose that for the any positive integer n , and x = T(x), {xn} and {yn} are the sequences of individuals with their genotype sequences {xn} and {yn}. T(y) < min (T(xn)[1/2] + T(yn)[1/2])

An Applicable Example

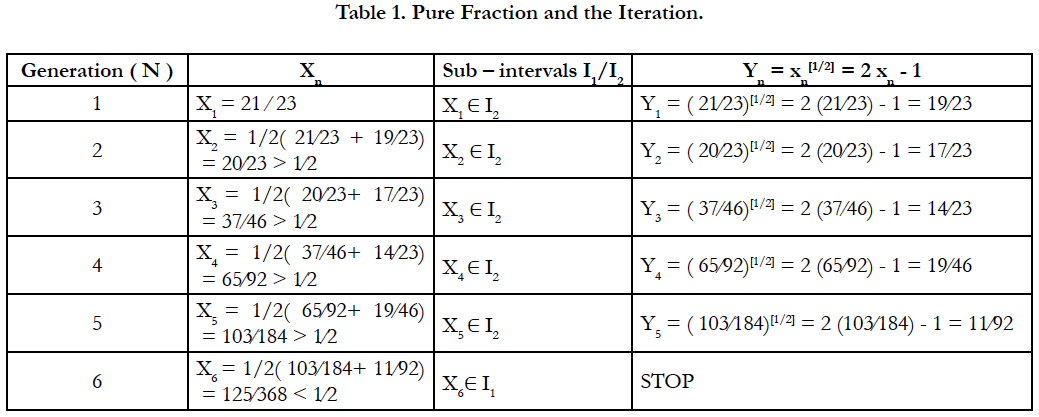
Suppose that X1= 21/23 ∈ [1/2, 1] = I2 be the pure fraction associated with an individual X. The iterative scheme and Theorem 4.4, and assumption 4.5 are used to find xN s.t:xN< 1⁄2. The iterations are given in the following Table (1).

---

---

Monte-Carlo Simulation

Monte Carlo Simulation or probability simulation is a very useful mathematical technique for analyzing uncertain scenarios and providing probabilistic analysis of different situations [16]. In general, the Monte Carlo simulation can be used to characterize any technique that approximates solutions to quantitative problems through statistical sampling. Also, this method utilizes iterative random sampling to produce simulated data to use with a mathematical model [13]. Mathematical models are one of analysis systems that use this technique.

To generalize the usefulness of the proposed approach to predict the number of generations needed to eliminate Thalassemia or other similar genetic diseases, Monte-Carlo Simulation via MATLAB will be used in this work. This approach of using both Fuzzy sets and discrete even simulation is not new, previous work has been done as in Zhang et al., [17].

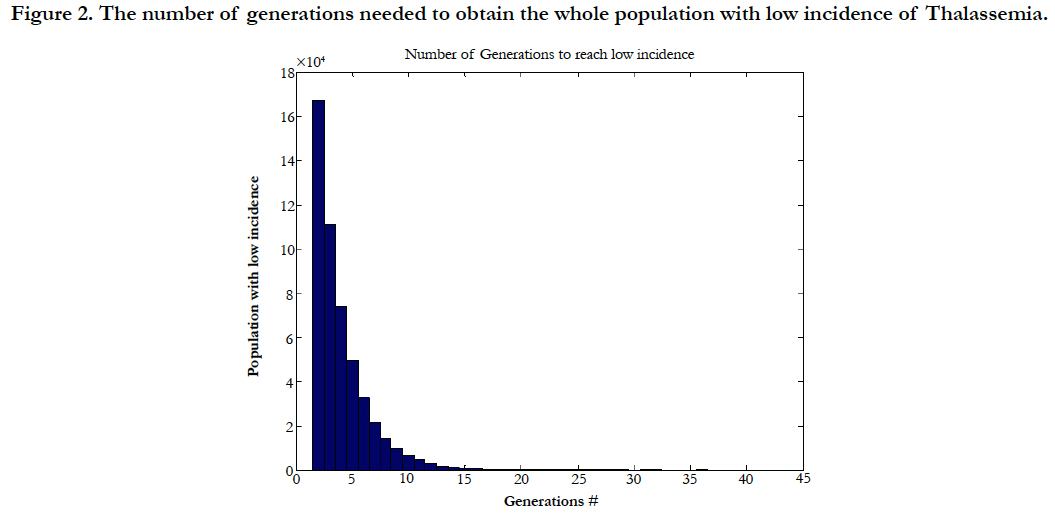
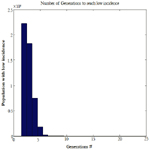
In this section we extend the calculations made in Section 6 to a population of 500,000 individuals with uniformly distributed, random and high incidence of the Thalassemia gene ∈ I2, the goal would be to evaluate how many generation needed so that all generated members of the final population have low incidence of the Thalassemia gene. As in Section 6 also we assume assumption 4.5 holds for choosing a partner. We model this problem using Monte Carlo simulation using MATLAB. For the purpose of demonstration we limit the number of children per generation to one child. Figure (2) shows the histogram for the number of generations needed so that the final generation has low incidence of the X gene. The mean number of generations needed to eliminate this gene based on our assumptions would be equal to 4 generations.

---

---

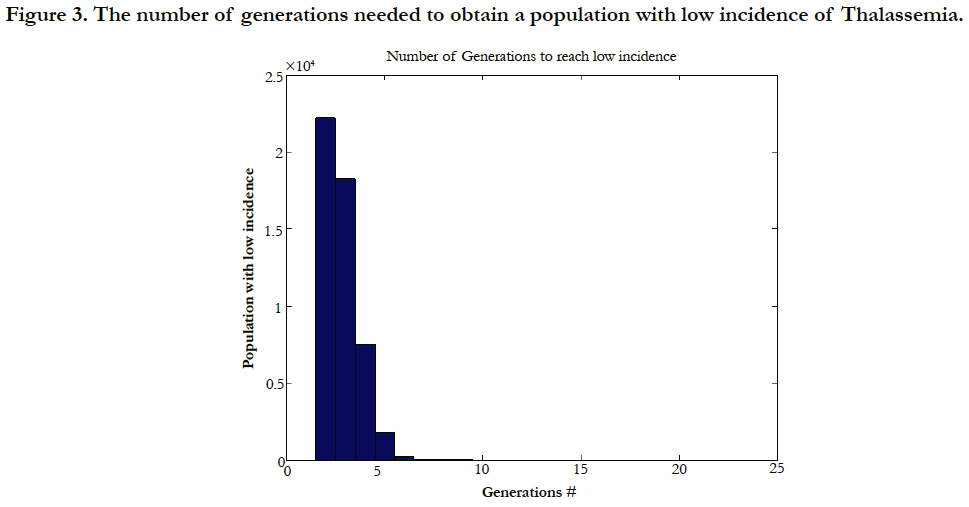
Of course, it is hard to obtain a partner with assumption 4.5 exactly holds. The assumption 4.5 should be thought of as an upper limit, i.e. if an individual wants to have a spouse/husband with Thalassemia gene, the spouse/husband's incidence should be less than or equal to the value obtained from assumption 4.5. If this modification is applied then we would expect to eliminate the disease in lesser number of generations than before. Figure 2 shows this new assumption and its corresponding results. Figure (3) shows the number of generations needed to obtain a population with low incidence of the Thalassemia disease with new policy applied. In this scenario, the average number of generations needed to eliminate the high incidence of the gene is just below 3 generations.

---

---

Results and Discussion

We constructed a mathematical modeling using pure fractions and Monte Carlo simulation to control Thalassemia Disease transition. An example in section 6 has been applied to demonstrate the simplicity of the technique. Through the computed iteration see Table 1, we have Xn s.t for generation N = 6, X6 < 1/2, hence X6 ∈ I1.

Therefore, after the 6th. Generation X1, and Y1 will have the descendant X6 who has a “low incidence” of the thalassemia gene g with genotype. The study of the genotypes for thalassemia disease which is a genetic disease is the motivation for the development of the mathematical model and the Monte Carlo Simulation. For this genetic disease, the people in danger are those with the genetypes X ∈ [1/2, 1]. The genotypes in [1/2, 1] are all reducible pure fractions. In this paper, the objective of creating this mathematical model is the controlling the transition of genes with “high incidence” genotypes to reach at genotypes X ∈ [0, 1/2] with “low incidence” so to get a healthy offspring from such a genetic disease over the future generations.

The mathematics of pure fractions was so appropriate for this objective. The theory of pure fractions is completely new in the sense in which the authors believe this work is the first study to formalize and standardize special structural properties of pure fractions. The theory shows potential for further research and applications. Particularly, the type of Genetic Remediation Scheme (GRS) can be modified to apply into many other genetic diseases. Monte-Carlo Simulation on the other hand proved these results by testing a large population of 500,000 individuals with the thalassemia gene.

Conclusion

In this research article, pure fraction plays a very useful role to control the transmission of thalassemia gene and to create a new generation without thalassemia Major or severe forms of thalassemia gene. Here, we adopt the concept of pure fraction to obtain a mathematical model that controls the thalassemia disease transmission. GRS can be determined depends on the value of Xn, if it is in the domain of I2 or I1. This model would help to the reduce thalassemia risk in future generation and to improve the medical care. The model was mathematically proved by the Monte-Carlo Simulation as well. Future outlooks could be extended to treat other variant infected and target cells.

1. What Are Thalassemias? NHLBI. July , 2012.
2. Cao A, Galanello R (2010) Beta-Thalassemia. Genet Med. 12(2): 61–76.
3. Jones, Daniel (2003) [1917], Peter Roach, James Hartmann and Jane Setter, eds., English Pronouncing Dictionary, Cambridge: Cambridge University Press, ISBN 3-12-539683-2.
4. What Is Anemia? – NHLBI, NIH. Jan, 2016.
5. Thalassemia, Mayo Clinic. October , 2014.
6. Complications- Thalassemia. Mayo Clinic. Feb, 2011.
7. HM Stark (1978) An Introduction to Number Theory, MIT Press, Boston.
8. BJ Strasser (1999) Sickle cell anemia a molecular disease. Sci. 286: 1488-1490.
9. LA Zadeh (1965) Fuzzy sets. Information and Control. 8: 338-353.
10. Klaua D (1965) Über einen Ansatz zur mehrwertigen Mengenlehre. Monatsb Deutsch Akad Wiss Berlin. 7: 859–876. A recent in-depth analysis of this paper has been provided by Gottwald, S. (2010). "An early approach toward graded identity and graded membership in set theory. Fuzzy systems. 161(18): 2369-2379.
11. Salii VN (1965) Binary L-relations. Izv Vysh Uchebn Zaved Matematika. 44(1): 133–145.
12. D Dubois, H Prade (1988) Fuzzy Sets and Systems. Academic Press, NewYork.
13. Eke B, Nkwanta A (2008) Mathematical model for the control of the transmission of genetic diseases using pure fractions. Int J Pure Appl Mathematics. 45: 243–54.
14. HT Nguyen, EA Walker (2005) A First Course in Fuzzy Logic . (3rd edn), Chapman & Hall - CRC, Boca Raton.
15. S Thakur, SN Raw1, R Sharma (2016) A Mathematical Model to Control the Transmission of Thalassemia Disease using Pure Fractions. Indian J Sci Technol. 9(4): 1- 5. DOI: 10.17485/ijst/2016/v9i2/78206.
16. Law AM, WD Kelton (2000) Simulation modeling & analysis. (3rd edn), McGraw-Hill, Inc, New York, USA.
17. Hong Zhang, CM Tam, Heng Li (2005) Modeling uncertain activity duration by fuzzy number and discrete-event simulation. Eur J Operation Res. 164(3): 715-729. http://dx.doi.org/10.1016/j.ejor. 2004.01.035.