Using Multiple Linear Regression and Artificial Neural Network to Predict Surface Roughness in Turning Operations

Keywords

Predictive; Turning; Artificial Neural Networks; Surface Roughness and Regression.

Introduction

Nowadays, due to the increasing demand of higher efficiency and quality, surface roughness of a machined part plays an important role in the modern manufacturing process. Machined surface characteristics affect the fatigue strength, corrosion resistance and tribological properties of machined components. The quality of material is determined by surface finish produced after machining. Therefore, control of the machined surface is essential to safe turning operations [1]. The quality of finished products is defined by how closely the finished product adheres to certain specifications, including dimensions and the quality of the surface [2]. Therefore, the most important aspects in manufacturing processes are measuring and characterizing of surface properties. Surface quality is defined and identified by the combination of surface finish, surface texture, and surface roughness. The surface roughness is one of the important properties of work piece quality in the turning process. Since the cutting conditions impact the quality of the surfaces, thus a work piece may be scrapped or reworked due to improper surface roughness machined. For this reason, several studies have been carried out to predict the value of roughness.

This study aims to develop two mathematical models to predict the surface roughness and to select the required surface roughness by using the Multi-regression model and ANN.

This paper is structured as follows: First, previous similar research is reviewed briefly. Then the experimental study is presented followed by modeling of surface roughness. Next, prediction and results are presented and analyzed. Finally, conclusions are made at the end of the paper.

Literature Review

Asiltürk and Cunkas [1] developed a model based on ANN and multiple regression to predict the surface roughness in AISI 1040 steel. It was found that the proposed models are capable of predicting the surface roughness. It was also found that the ANN model estimates the surface roughness with high accuracy compared to the multiple regression model.

Asiltürk and Neseli [3] developed a model to determine the effect of cutting parameters, namely cutting speed, depth of cut and feed rate on surface roughness during machining of AISI 304 austenitic stainless. The conclusion of the study was that the feed rate is the dominant factor affecting the surface roughness, which is minimized when the feed rate and depth of cut are set to the lowest level, while the cutting speed is set to the highest level. The percentages of error fall within 1% between the predicted values and the experimental values.

Patel et al., [4] developed a mathematical model by using ANN technique to predict surface roughness in CNC milling machine. Several experiments were carried out by using HSS CNC milling machine. The input parameters of the ANN are spindle speed, feed rate and depth of cut. The results showed that the prediction of surface roughness is accurate by 91.94% [4].

Parmar and Makwana [5] developed a model to predict surface roughness by using artificial neural networks. The aim of the study was to find the best cutting parameters value for a specific cutting condition in milling operation and achieve minimum surface roughness. Experimental investigation was conducted using the end milling of mild steel material up to 30 HRC with carbide tool by varying feed rate, speed and depth of cut. The surface roughness was measured using Mitutoyo Surface Roughness Tester. The results of the study were as follows: the maximumsurface roughness value 0.35μm was obtained at the value of 0.06 mm/rev, 80 m/min and 0.2 mm for feed rate, cutting speed and depth of cut respectively.

Aghdeab et al., [6] developed a model to obtain the optimal parameters of CNC turning process that lead to an optimal surface roughness for machining aluminum alloy ENAC43400. The developed objective model was obtained using the regression method and optimized by the simulated annealing method in order to determine the best set of turning parameter values. It was found that the surface roughness is about (1.06-1.41μm).

Tsao [7] adopted grey Taguchi method to optimize the milling parameters of A6061P-T651 aluminum alloy with multiple performance characteristics. The experimental results indicated that the optimal process parameters in milling aluminum alloy can be effectively determined; the flank wear was decreased from 0.177 mm to 0.067 mm and the surface roughness was decreased from 0.44 μm to 0.24 μm. This result led to a multiple performance characteristics improvement in milling qualities through the grey Taguchi method.

Fang et al., [8] conducted a study dealing with the neural network modeling and prediction of surface roughness in machining aluminum alloys using data collected from both force and vibration sensors. Two neural network models, including a Multi-Layer Perceptron (MLP) model and a Radial Basis Function (RBF) model, were developed. Each model includes eight inputs and five outputs. The eight inputs include the cutting speed, the ratio of the feed rate to the tool-edge radius, cutting forces in three directions, and cutting vibrations in three directions. The five outputs were the five surface roughness parameters. The results of the study showed that the MLP model provided significantly higher accuracy of prediction for surface roughness than the RBF model did.

Kumar and Narayana [9] developed a model based on a combination of three soft computing techniques namely Adaptive Neuro Fuzzy Inference System, Neural Networks and regression to predict the surface roughness in turning process. The input variables of the model are the machining variables that have a major impact on the surface roughness in turning process such as spindle speed, feed rate and depth of cut. On the other side, surface roughness is considered as output. Based on the experimental results of the study, it was observed that surface roughness value increases as the feed rate and depth of cut increases and as the spindle speed increases the surface roughness value decreases. It was also found that the minimum surface roughness value is observed at spindle speed of 150 rpm, feed rate of 0.05 mm/rev and a depth of cut of 0.2 mm respectively.

Dinesh et al., [10] developed an empirical model using Response Surface Methodology to predict material removal rate (MRR) and surface roughness in CNC turning of EN24 Alloy Steel. The influence of four cutting parameters, cutting speed, feed rate, depth of cut, and tool nose radius on minuscule surface roughness and MRR were analyzed on the basis of Response Surface Methodology approach. It was found that the surface roughness is (0.43-1.99 μm). Also, it was found that the minimum speed of 110m/min produces higher MRR. The depth of cut has an inverse effect on MRR. The maximum depth of cut of 1.0 mm produces higher MRR. Hence higher MRR was achieved by combining minimum feed rate and maximum depth of cut.

Experimental Study

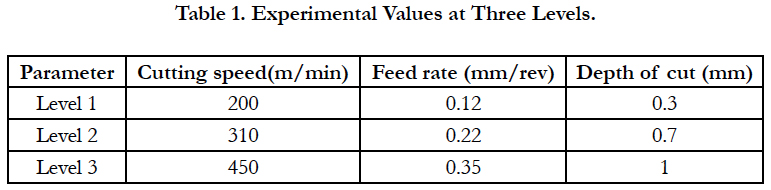
This section studys the selection of parameters which affect the surface roughness values, type of work piece material and experimental plan required to conduct the experiment. In turning, the speed and motion of the cutting tool is specified through several parameters. These parameters are selected for each operation based upon the work piece material, tool material, tool size, and others. Turning parameters that can affect the process are: spindle speed, feed rate and depth of cut. The parameters to be considered in the study were identified at three levels for each of these factors, as shown in Table (1).

---

---

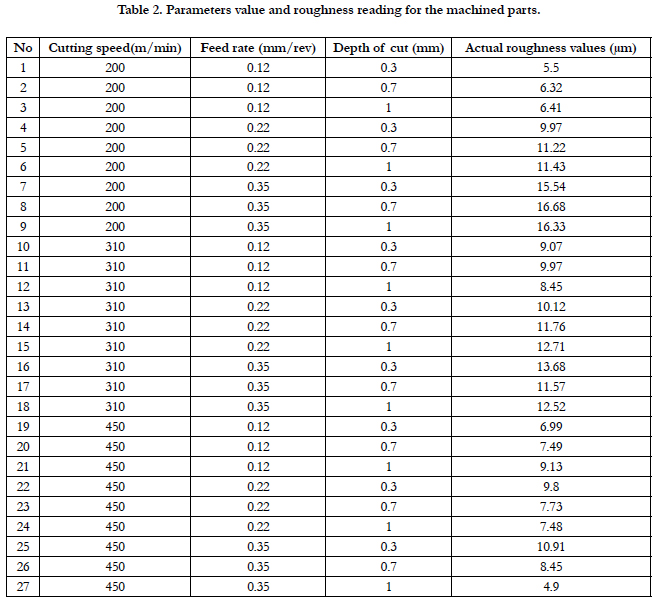
In order to test the developed models, 27 pieces of alloy steel HRC15 were operated and the roughness of their surfaces measured by ALPA-SM RT-20. The running of the three test pieces was based on random cut conditions. The experiments were carried out using CNC turing machine TLC-20B.

Modeling of Surface Roughness

In this paper, two models are developed based on Multi-regression model and Artificial Neural Networks to predict surface roughness. The two models have been solved using Microsoft excel and Neuro software.

Regression Model

The regression model for multiple regression line is shown in Equation (1) [11].



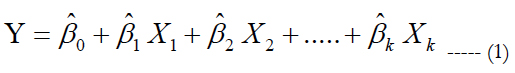
Where:

Y: dependent variable;
ˆβ0: Constant or intercept;
ˆβk: regression slope of Y on independent variable Xk;
Xk : Independent variable.

The regression model is solved by using experimental data, and then roughness values can be predicted. The accuracy of the results of the multiple linear regression model can then be evaluated using R adjusted Square. Also it can be evaluated using F test significance. If the value of F is less than or equal to 0.05, this means that the model is statistically acceptable. In the contrary, if the value is more, then the model is unacceptable.

Artificial Neural Networks Modeling

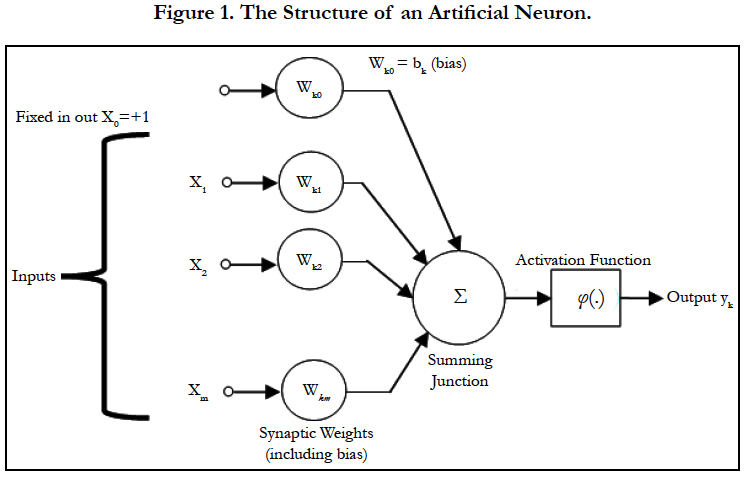
Neural network is a highly flexible modeling tool with the ability to learn the mapping between input and output parameters [5]. The main concept of Artificial neural networks (ANNs) is based on emulating the biological connections between neurons. ANNs can reproduce some functions of human behavior, which are formed by a finite number of layers with different computing elements called neurons. In order to construct a network, the neurons are interconnected. As shown in Figure (1), the network consists of an input layer used to present data, output layer to produce ANN’s response, and one or more hidden layers in between. The organization of connections determines the type and objectives of the ANNs. The processing ability of the network is stored in the inter-unit connection strengths, or weights, which are tuned in the learning process. The learning algorithm is defined as a procedure that consists of adjusting the weights and biases of a network that minimizes selected function of the error between the actual and desired outputs [1].

---

---

The steps of the learning algorithm of ANN with backpropagation algorithm is as follows [12]:

Step 1: Initialization of the initial weights (w1, w2, w3, ......, wn) = Wn and Θ represents the threshold.

Step 2: Select learning vector pair (Xn, Yj), where Xn represents input vector.

Xn = (x1, x2, x3, …., xn)

Yj : Represents the required output

Yj = (y1, y2, y3, …., yj)

Step 3: Calculating the real output value as follows:

1) Calculate the real output value from the input layer to the hidden layer.



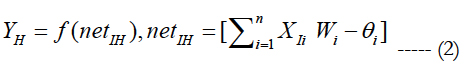
n: represents the number of elements in the input layer of the network.

2) Calculate the real output value of the hidden layer to the output layer.



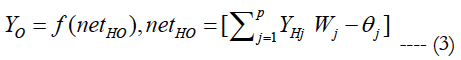
P: represents the number of elements in the hidden layer of the network.

Step 4: Calculate the error as follows:



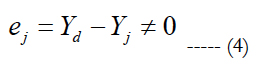
d: the real value of the roughness.

1) The weights between the output layer and the hidden layer can be modified as follows:



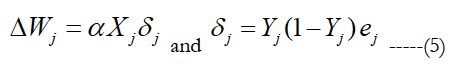
2) The weights between the hidden layer and the input layer can be modified as follows:



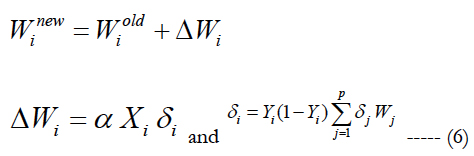
Step 5: Repeat the steps from step 2 through step 5 until the desired convergence is obtained, which represents the lowest square rate.

Prediction of Results and Analysis

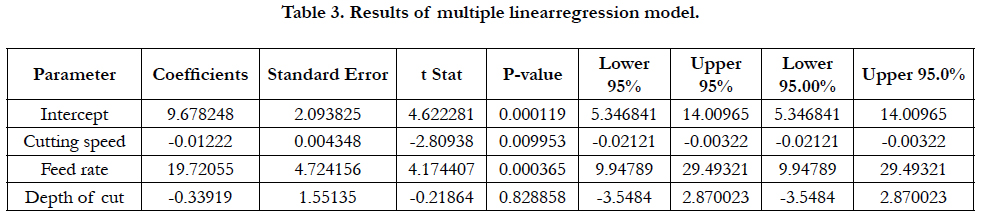
The experiments were conducted for three different levels for each variable, the total number of (27) pieces of alloy HRC15. Table (2) shows the input data for the experiment and the reading values for surface roughness. The multiple linear regression equation constants is obtained by using Excel program. Input experiment data (Speed, Feed rate, and Depth of cut) and the corresponding output data (Experimental roughness data) were entered to the regression model. Table (3) shows results of multiple linear regression model.

---

---

---

---

Based on the results of Table (3) the regression equation is given by equation (1).

Y = 9.678248 + (-0.01222 X1) + (19.72055 X2) + (-0.33919 X3) (1)

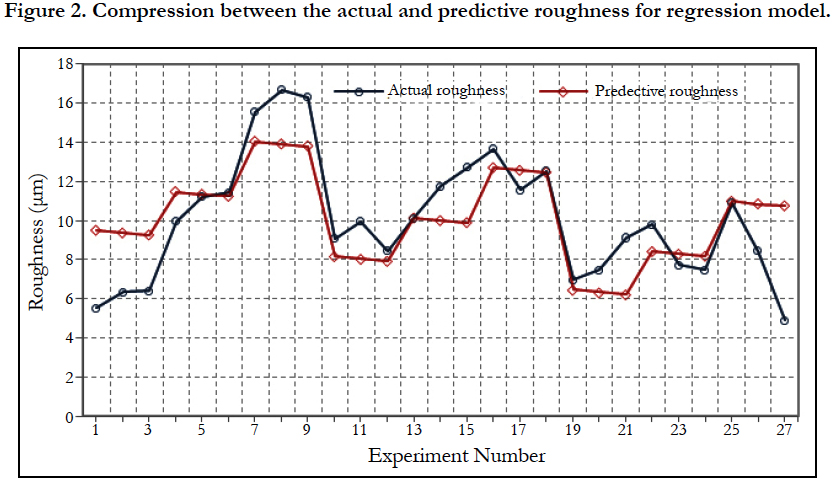
Figure (2) shows the real roughness (measured) values and the roughness obtained from the Multi-regression model for the number of experiments. It is seen from Figure (2) that there is a strong relationship between the predictor variables and response variable.

---

---

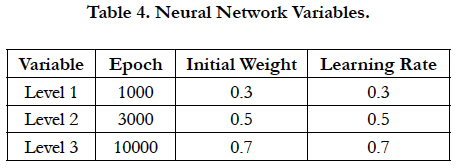
To develop artificial neural networks model, there are many variables that effect the development of ANN and they must be identified when creating the network. These variables are as follows:

1) Epoch: variable is used to stop learning, where the network stops learning if the number of iterations reach to the number of iterations specified.
2) Learning Rate (tr): learning rate and determines the speed of change of inclination and bias. The bias can be considered as one of the weights of W0 and its input (X0 = 1).
3) Initial Weight: The primary weight in the training process.
The previous variables were determined when the network was created. Thus, 27 networks were created for each network containing different variables from the other network. For the purpose of finding optimal variables for the best solution for the 27 pieces by finding the error ratio. Three by finding the error rate. Table (4) shows the three variables of the network and its different levels.

---

---

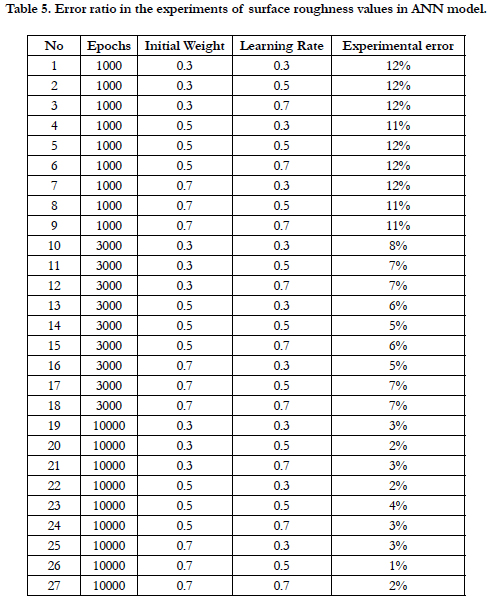
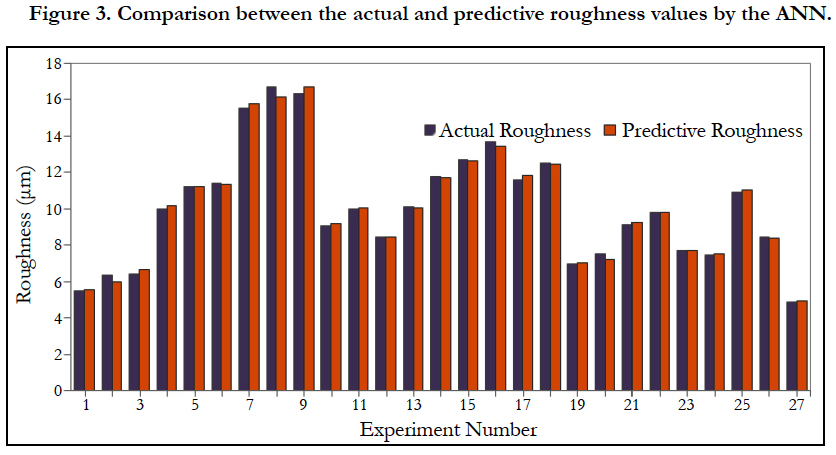
The artificial neural network model was solved using Neuro software to learn the network and obtain the predictive roughness values of the network. Table (5) shows the error rate when changing the value of the three variables mentioned in Table (4). The network with the lowest error rate and the lowest error ratio were selected at experiment number 26. Figure (3) shows a comparison between the real and predicted values of roughness by the artificial neural network model.

---

---

---

---

Conclusion

In this study, multiple regression and artificial neural network approaches were used to predict the surface roughness of alloy steel HRC15. Regarding to the value of P of multiple linear regression model it can be concluded that the most influential factor on surface roughness is the amount of feed rate and then the cutting speed. On the other hand, the depth of cut is the least. The value of F test signal was much smaller than 0.05 which means that the model is statistically acceptable. The predicted values obtained from the artificial neural network model were better than the multiple linear regression model by error of 1% and 20%, respectively. The most significant variable when developing the network in the artificial neural network model was epochs, where the error rate was 11% at number of iterations 1000 to 1% at number of iterations 10,000. The proposed models can be used effectively to predict the surface roughness in turning process. Considering the advantages of the ANN compared to multiple regression are simplicity, speed, and capacity of learning, the ANN is a powerful approach in predicting the surface roughness.