Biomarker - Driven Adaptive Design for Precision Medicine
Wang J1, Chow SC2, Chang M3,4*
1 Biostatistics, Gilead Sciences, Inc., Foster City, CA, USA.
2 Department of Biostatistics & Bioinformatics, Duke University, Durham, NC, USA.
3 Strategic Statistical Consulting, Veristat, Southborough, MA, USA.
4 Department of Biostatistics, Boston University, Boston, MA, USA.
*Corresponding Author
Mark Chang,
Adjunct Professor, Biostatistics, Department of Biostatistics,
Boston University, Boston, MA, USA.
E-mail: Mark.Chang@veristat.com
Received: November 09, 2016; Accepted: November 17, 2016; Published: November 19, 2016
Citation: Wang J, Chow SC, Chang M (2016) Biomarker - Driven Adaptive Design for Precision Medicine. J Translational Biomarkers Diagn. 2(1), 15-24.
Copyright: Chang M© 2016. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.
Abstract
Recent advances in genetic engineering have made a finer taxonomy of disease possible, which enables the development of precision medicine. In this article, we give an overview of biomarker-driven clinical trial designs, with a focus on adaptive designs so as to increase the power and efficiency to detect an effective therapy. Biomarker-driven designs are also useful in studying rare diseases.
2.Introduction
3.Classical Designs
3.1.Biomarker - Enrichment Design
3.2.Biomarker Stratified Design
3.3.Sequential Testing Strategy Design
3.4.Marker-based Strategy Design
3.4.Hybrid Design
4.Adaptive Designs
4.1.Adaptive Accrual Design
4.2.Biomarker-Adaptive Threshold Design
4.3.Adaptive Signature Design
4.4.Cross-Validated Adaptive Signature Design
4.5.Bayesian Adaptive Randomization Enrichment Design
5.Discussion
6.References
Keywords
Adaptive Design; Biomarkers; Clinical Trials; Personalized Medicine; Drug Development.
Introduction
Traditional clinical development of a novel therapy utilizes the “one-size-fits-all” approach by testing treatment effect in the entire patient population with a specific disease. It assumes that response in the disease population is homogeneous. In his State of the Union address in early 2015, President Obama announced that he is launching the Precision Medicine Initiative - a bold new research effort to revolutionize how we improve health and treat disease. President Obama pointed out that precision medicine is an innovative approach that takes into account individual differences in people’s genes, environments, and lifestyles. Unlike traditional approach, precision medicine proposes the customization of healthcare, with medical decisions, practices, and treatments being tailored to the individual patient.
Recent advances in genetic engineering such as DNA sequencing and mRNA transcript profiling has made a finer taxonomy of disease possible, which enables the development of precise diagnostic, prognostic, and therapeutic paradigms for specific subsets of patients for achieving the ultimate goal of precision medicine. Thus, these targeted therapies may benefit only a subset of the entire patient population and may not benefit or even harm the rest of the population. On the other hand, biomarkers have the potential to provide substantial added value to the current medical practice for the purpose of precision medicine. Biomarkers are widely expected to be used as a tool in drug discovery, understanding the mechanism of action of a drug, investigating efficacy and toxicity signals at an early stage of pharmaceutical development, and in identifying patients likely to response to treatment.
As a result of these new opportunities and challenges, the traditional paradigm of drug development not taking into account response heterogeneity may be suboptimal. To embark on the mission of precision medicine, innovative statistical designs utilizing biomarker enrichment strategies (“biomarker-driven clinical trial designs”) are becoming increasingly attractive. The term enrichment is defined as “the prospective use of any patient characteristic to select a study population in which detection of a drug effect (if one is in fact present) is more likely than it would be in an unselected population”. (FDA, 2012).
The study of rare diseases fits the model of precision medicine naturally: at least 80% of them arise from genetic variations, and show varying degree of heterogeneity from patient to patient [13]. Thus, biomarker-driven clinical trials are useful in studying rare diseases, especially when the availability of patients with rare diseases is limited. Biomarkers have the potential of helping in identifying patients which are most likely to respond to the test treatment under investigation. Consequently, biomarker- driven designs may result in (1) smaller study sizes, (2) higher probability of trial success, and (3) enhancement of the benefitrisk relationship.
In the past decade, precision medicine and biomarker-driven clinical trials have been discussed and studied by many authors in the literature, e.g., Hawgood et al., (2015) [14], Collins and Varmus (2015) [10], Jameson and Longo (2015) [16], Bayer and Galea (2015) [2], Mirnezami et al., (2012) [35], Simon and Maittournam (2004) [25], Mandrekar and Sargent (2009) [20], Weir and Walley (2006) [35], Simon (2010) [24], and Baker et al., (2012) [1]. In practice, biomarker-driven adaptive designs are adaptive designs that allow us to select target population based on interim data [26]. Simon and Wang (2006) [27] and Freidlin, Jiang and Simon (2010) [11] studied a genomic signature design, Jiang, Freidlin and Simon (2007) [4] proposed Biomarker-adaptive threshold design, Chang (2006, 2007) [5], Wang et al., (2007) [33], Wang, Hung and O'Neill (2009) [34] and Jenkins et al., (2011)[17] studied population enrichment design using biomarker, which allow interim decision on the target population based on power or utility. Zhou et al., (2008) [37] studied Bayesian adaptive randomization design that provides patients with potentially more effective treatments. Song and Pepe (2004) [28] studied markers for selecting a patient's treatment. Studies on biomarker-adaptive design were done by Beckman, Clark, and Chen (2011) [3]for oncology trials. Recently, Wang (2013) [30], Wang, Chang, and Menon (2014, 2015) [31, 32] using a two-level relationship between continuous biomarker and the primary endpoint to solve the mystery why the first level correlation play a limited role in adaptive design.
In this article, we give an overview of biomarker-driven clinical trial designs utilizing predictive biomarker enrichment strategies that are growing in the statistical literature, with a focus on adaptive designs so as to increase the power and efficiency to detect an effective therapy with regard to a predictive biomarker in clinical trial. A predictive biomarker is type of biomarker that identifies patients who are likely to benefit from a particular treatment, in contrast to a prognostic biomarker which is associated with only the disease outcome. Biomarkers can be used in two-group design and multi-group (pick-the-winner, drop inferior arms, and addarm) enrichment design [23, 32]. However, we will focus on the two-group designs.
Classical Designs
The biomarker-enrichment design is a randomized design involving only patients with a specific biomarker status (Freidlin et al., 2010; Sargent et al., 2005; Chang, 2006, 2007) [4, 5, 11, 22]. This design is most appropriate when the mechanistic behavior of drug is known and there is compelling preliminary evidence of benefits in a subgroup of patient population defined by a specific biomarker status.
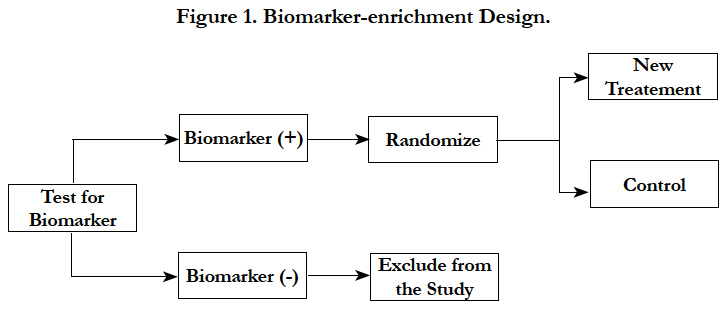
In biomarker-enrichment design, patients are screened for the presence or absence of a biomarker(s) profile. After extensive screening, only patients with the presence of a certain biomarker characteristic or profile are enrolled in the clinical trial. In principle, this design essentially consists of an additional criterion for patient inclusion in the trial (Figure 1) [15].
A recent example for the enrichment design was of mutated BRAF-kinase [7]. Almost 50% of melanomas have an activating V600E BRAF mutation. This leads to the hypothesis that inhibition of mutated BRAF kinase will have meaningful clinical benefit. Hence only patients who tested positive forV600EBRAF mutation were enrolled in the study. Patients were randomized to an inhibitor of mutated BRAF-kinase or control treatment. As hypothesized, the large treatment benefit was observed in the pre-specified subgroup.
The following considerations should be taken into account in this design – 1) during the conduct of the study, it is important to have rapid turnaround times for the assay results in order to enroll patients faster; 2) the assay testing should be consistent between different labs; 3) restricted enrollment does not provide data to establish that treatment is ineffective in biomarker negative patients; 4) a low prevalence of the marker may be challenging operationally and financially.
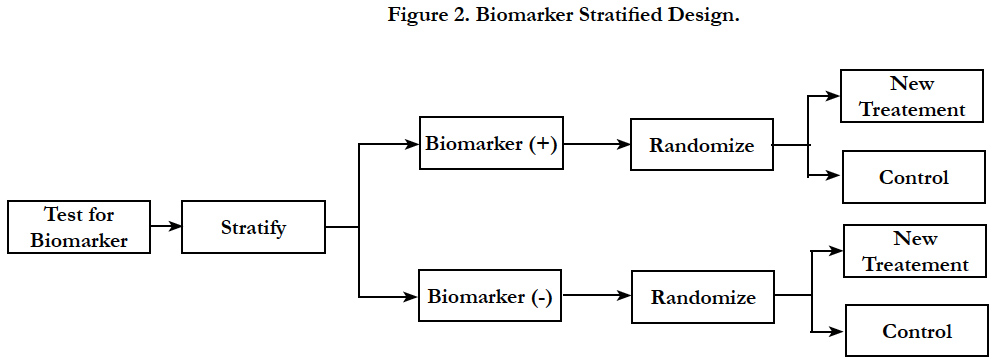
In biomarker stratified design, patients are tested for biomarker status and then separately randomized according to their positive or negative status of the marker [11]. This design is chosen when there is no preliminary evidence to strongly favor restricting the trial to patients with specific biomarker profile that would necessitate a biomarker-enrichment design.
In biomarker stratified design, randomization is done using marker status as the stratification factor; however only the patients with a valid measurable marker results are randomized (Figure 2). Two separate hypotheses tests are conducted to determine the treatment effect within each biomarker group. The sample size is calculated separately to power the testing within each biomarker group. Another variation to the hypothesis test within the same design is to conduct a formal marker by treatment interaction test to see if the treatment effect varies within each marker status subgroup. In this case, the study is powered based on the magnitude of interaction.
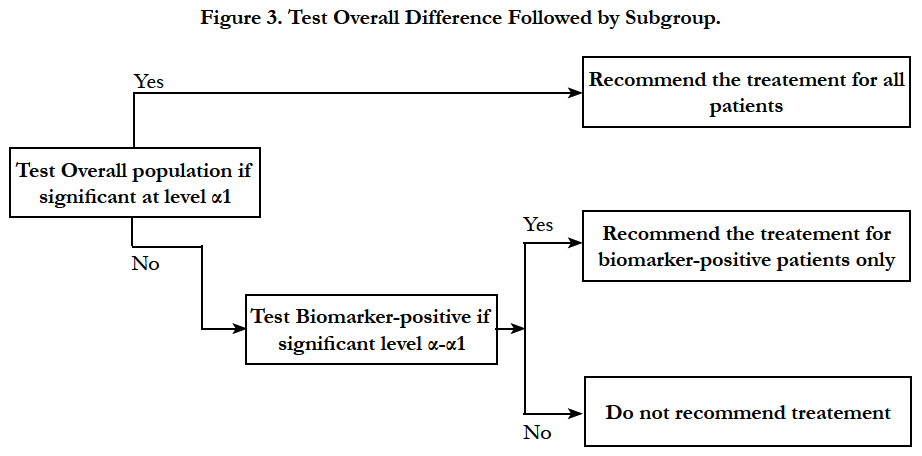
Sequential testing strategy designs can be viewed as a special case of the classical randomized clinical trial for all comers or unselected patients. In this design, randomization is not stratified by biomarker status. Thus, sample sizes in the treatment groups within each biomarker defined subgroup should be large enough to balance important prognostic baseline factors to ensure effective results. Two testing strategies are frequently used: test overall difference followed by subgroup; test subgroup followed by overall population.
Simon and Wang (2006) [27] proposed an analysis strategy where the overall hypothesis is tested first to see if there is a difference in the response in new treatment versus the control group in entire patient population. If there is no difference and the response is not significant at a pre-specified significance level (for example 0.04), then the new treatment is compared to the control group in the biomarker positive patients. The second comparison uses a threshold of significance which is proportion of the traditional 0.05 not utilized by the initial test (for example 0.01). This approach is useful when the new treatment is believed to be effective in a wider population, and the subset analysis is supplementary and used as a fall back option (Figure 3).
Song and Chi (2007)[29] later proposed a modification of the above method. Their method takes into account the correlation between the test statistics of the hypotheses of the overall population and the biomarker positive population.
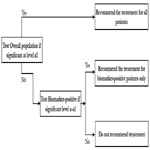
In this analysis strategy, the hypothesis for the treatment is first tested in the biomarker positive status patients and then tested in the overall population. This strategy is appropriate when there is a preliminary biological basis to believe that biomarker status positive patients will benefit more from the new drug and there is sufficient marker prevalence to appropriately power the trial. Study would be powered for effect in biomarker positive status group and the size of biomarker negative status group could be determined separately to allow a reasonable estimate of effect in marker negative group. In this closed testing procedure, the final type I error rate is always preserved (Figure 4).
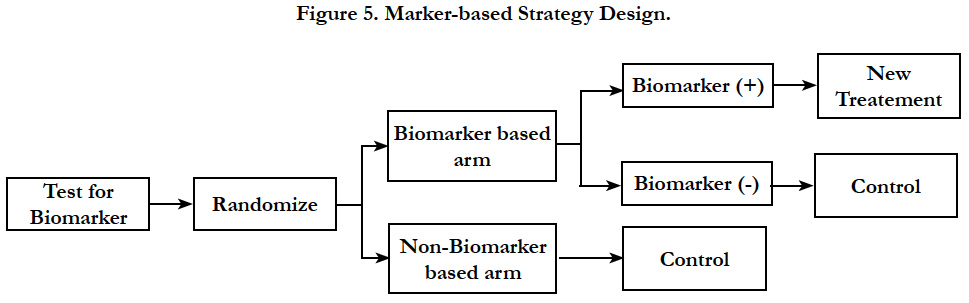
In this design, patients are randomly assigned to treatment dependent or independent of the marker status (Figure 5). All patients randomized to the non-biomarker based arm receive the control treatment. In the biomarker based arm, the biomarker positive patients will receive the experimental therapy while biomarker negative patients receive control treatment [11, 22].
The outcome of all of the patients in the marker based subgroup is compared to that of all patients in the non-marker based subgroup to investigate the predictive value of the marker. One downside of this design is that patients treated with the same regimen are included in both the marker-based and the non–markerbased subgroup, resulting in a substantial redundancy. Another disadvantage is the inability to examine the effect of targeted therapy in biomarker negative patients as none of these patients receive it. The treatment difference between the new treatment and the control treatment can be diluted by marker-based treatment selection and sometimes can be a poor choice as compared to the randomized design.
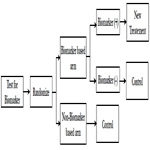
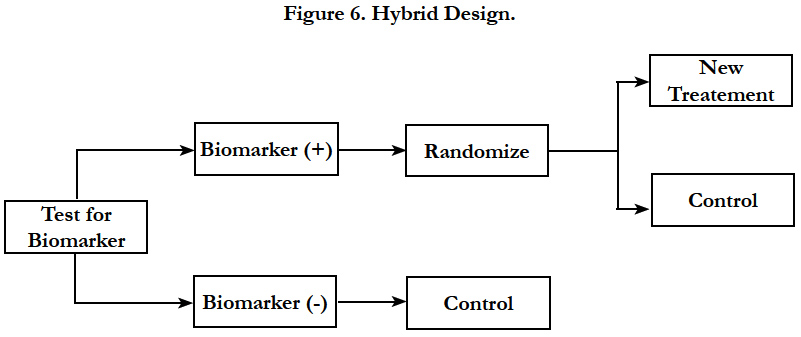
Hybrid design should be considered when there is compelling prior evidence demonstrating the efficacy of a certain treatment for a biomarker subgroup renders it unethical to randomly assign patients with that particular biomarker status to other treatment options. In this design, only marker-positive patients are randomly assigned to treatments, whereas patients in the marker-negative group are assigned to control or standard-of-care treatment (Figure 6). The study is powered to detect treatment difference only in the marker-positive group. However, samples are collected from all the subjects to help testing for additional markers in the future.
As a summary of the above classical designs we reviewed, Table 1 lists relative merits and limitations of each design.
Adaptive Designs
According to the NIH Office of Budget, the investment in pharmaceutical research and development has more than doubled in the last two decades. However, the success rate for new drug applications (NDAs) remains low. As reported by the U.S. Government Accountability Office (GAO), the approval rate for NDAs submitted to the FDA in 2009 is only about 40%. Reasons for this include [36]: (i) a diminished margin for improvement has escalated the level of difficulty in proving drug benefits; (ii) genomics and other new science have not yet reached their full potential; (iii) mergers and other business arrangements have decreased candidates; (iv) easy targets are more difficult to study; (v) rapidly escalating costs and complexity have decreased willingness to bring many candidates forward into the clinic. United States Food and Drug Administration (FDA) hosted a “Critical Path Initiative” to identify key scientific challenges underlying the medical product pipeline problems and released a Critical Path Opportunities List in 2006 that encouraged advancement of innovative clinical trial designs especially learning from prior experience and ongoing accumulated data. The innovation implies the use of adaptive design methods and the potential use of Bayesian approach. Chow et al., (2005)[8] define adaptive design as “a design that allows adaptations or modifications to aspects of the trial after its initiation without undermining the validity and integrity of the trial”. The PhRMA Working Group refers an adaptive design as a clinical study design that uses accumulating data to direct modification of aspects of the study as it continues, without undermining the validity and integrity of the trial [12]. Nowadays, the application of adaptive design methods in clinical trials has become very popular due to its flexibility and efficiency.
Some of the commonly used prospective pre-specified adaptive designs include (i) Group sequential design, (ii) sample size reestimation design, (iii) adaptive seamless design, (iv) drop-theloser design, (v) adaptive randomization design, (vi) adaptive dose-finding design, (vii) biomarker-adaptive design, (viii) adaptive treatment-switching design (ix) hypothesis-adaptive design, (x) any combinations of the above. (Chow and Chang, 2011)[9]. In this section, we will review adaptive designs related to biomarker selection and enrichment.
If biomarker-based subgroups are predefined, but with uncertainty on the best possible endpoint and population, an adaptive accrual design could be considered with interim analysis that may lead to modify the patient population to accrual.
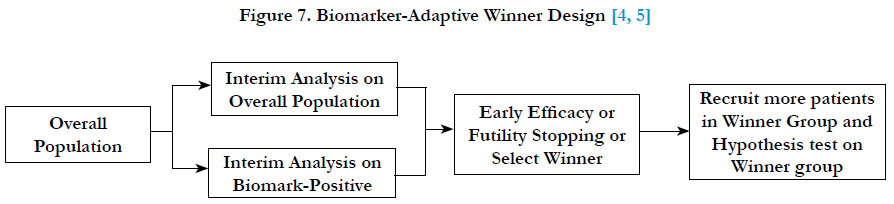
Chang (2006, 2007)[4, 5] proposed an adaptive accrual design which is called a “biomarker-adaptive winner design” for oncology trials. In this design, the recruitment starts with overall patient population, at interim analysis, select either biomarker-positive or overall population as the winner population and continue to recruit the winner population at the second stage of the trial. In the final analysis, the hypothesis test will be conducted on the winner population. The winner can be determined based on effect sizes, the interim p-values, conditional powers, or utility functions of the population group (Figure 7).
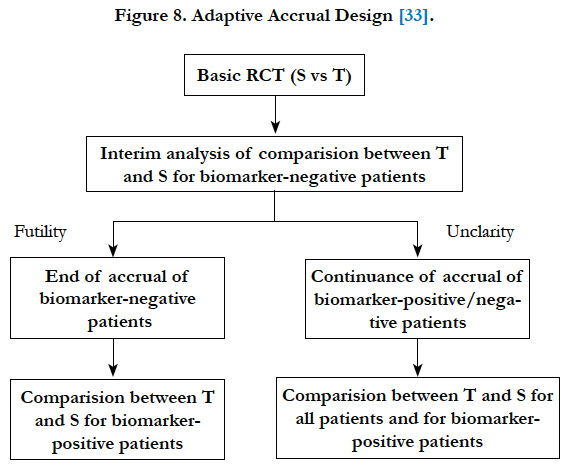
Wang et al. (2007)[33] proposed a phase III design comparing an experimental treatment with a control treatment that begins with accruing both positive and negative biomarker status patients. An interim futility analysis would be performed, and based on results of the interim analysis it is decided to either continue the study in all patients or only the biomarker positive patients. Specifically, the trial follows the following scheme: begin with accrual to both marker-defined subgroups; an interim analysis is performed to evaluate the test treatment in the biomarker-negative patients. If the interim analysis indicates that confirming the effectiveness of the test treatment for the biomarker-negative patients is futile, then the accrual of biomarker-negative patients is halted and the final analysis is restricted to evaluating the test treatment for the biomarker-positive patients. Otherwise, accrual of biomarkernegative and biomarker-positive patients continues to the target sample size until the end of the trial. At that time, the test treatment is compared to the standard treatment for the overall population and for biomarker-positive patients (Figure 8).
Figure 8. Adaptive Accrual Design [33].
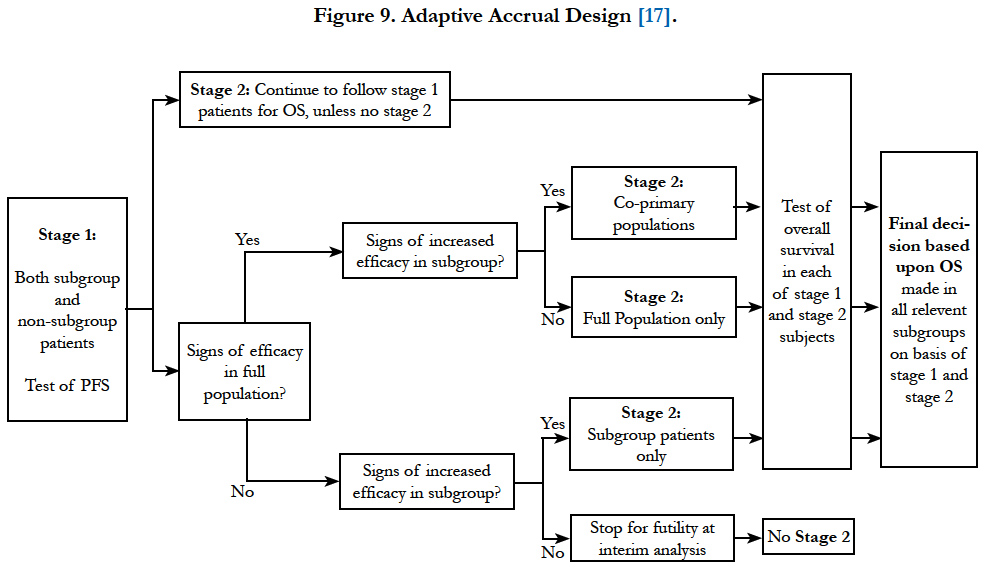
Jenkins et al., (2011)[17] proposed a similar design but with more flexibility. It allows the trial to test treatment effect in the overall population, subgroup population or the co-primary populations at the final analysis based on the results from interim analysis. Besides, the decision to extend to the second stage is based on intermediate or surrogate endpoint correlated to the final endpoint (Figure 9). In this design, a combination of test statistics for the final endpoint from each stage is used for hypothesis testing. The patients who start in the first stage will remain in the study and would be monitored for their long term (final) endpoint.
Figure 9. Adaptive Accrual Design [17].
Biomarker development and validation is usually very expensive and time consuming. Often times by the time of the start of late phase clinical trials, a reliable biomarker, as well as its threshold, for identifying patients sensitive to an experimental treatment is not known.
When the marker is known but the threshold or the cut point for defining a positive or negative biomarker status is not clear, a biomarker-adaptive threshold design can be considered [18]. The biomarker-adaptive threshold design combines the test of overall treatment effect with the establishment and validation of a cut point for a pre-specified biomarker which identifies a biomarker-based subgroup believed to be most sensitive to the experimental treatment. This design potentially provides substantial gain in efficiency.
Specifically, the main purpose of the biomarker-adaptive threshold design is to identify and validate a cut-off point for a prespecified biomarker, and to compare the clinical outcome between experimental and control treatments for all patients and for the patients identified as biomarker positive in a single study. The procedure provides a prospective statistical test of the hypotheses that the experimental treatment is beneficial for the entire patient population or that the experimental treatment is beneficial for a subgroup defined by the biomarker, and provides an estimate of the optimal biomarker cut-off point.
The statistical hypothesis test can be carried out by splitting the overall type I error rate α. First, compare the treatment response on the overall population at α1 and if not significant then perform the second test at α- α1. For example, if the null hypothesis of no benefit in overall population is rejected at a desired significance level of say 0.04 then the testing is stopped. Otherwise, the testing is carried out at 0.01 to test the hypothesis of no benefit in identified biomarker-based subpopulation. This strategy controls overall alpha below the 0.05 level. The advantage of this procedure is its simplicity and that it explicitly separates the effect of the test treatment in the broad population from the subgroup specification. However, it takes a conservative approach in adjusting for multiplicity in combining the overall and subgroup analyses. Other strategies of combining the two statistical tests for overall and subgroup patients involve consideration of the correlation structure of the two test statistics. A point estimate and a confidence interval for the cut-off value could be estimated by a bootstrap re-sampling approach.
The adaptive signature design [11] is a design proposed to select the subgroup using a large number of potential biomarkers. This design is appropriate when both the potential biomarkers and the cut off are unknown however there is some evidence that the targeted therapy may work in some of the shortlisted biomarkers.
It combines a definitive test for treatment effect in entire patient population with identification and validation of a biomarker signature for the subgroup sensitive patient population. There are three elements in this design: (a) trial powered to detect the overall treatment effect at the end of the trial; (b) identification of the subgroup of patients who are likely to benefit to the targeted therapy at the first stage of the trial; (c) statistical hypothesis test to detect the treatment difference in sensitive patient population based only the subgroup of patients randomized in the latter half of the trial. These elements are pre-specified prospectively.
Statistical tests should be conducted appropriately in this design to account for multiplicity. A proposed strategy is as follows: test the initial null hypothesis of no treatment benefit in overall population at a slightly lower significance level than the overall alpha of 0.05 (for example, 0.04). If the initial null hypothesis is rejected at the lower significance level, then the targeted therapy is declared superior than the control treatment for the overall population. The hypothesis testing and analysis is complete at this stage. If the first hypothesis is not rejected, then the signature component of the design is used to select a potentially promising biomarker subgroup. It is done by the following steps: split the study population into a training sub-sample and a validation sub-sample of patients. Training sub-sample is used to develop a model to predict the treatment difference between targeted therapy and control as a function of baseline covariates. The developed model is then applied to validation sub-sample to obtain the prediction for each subject in this sample. A predicted score is calculated to classify the subject as sensitive or non-sensitive. The subgroup is selected using a pre-specified cut-off for this predicted score. The second hypothesis test is conducted in this sensitive subgroup to see the benefit of the targeted therapy against the control. This test is conducted at a much lower significance (for example, 0.01). According to Freidlin and Simon (2009)[11], this design may be ideal to use for Phase II clinical trials for developing signatures to identify patients who respond better to targeted therapies. The advantage of this design is its ability to de-risk losing the label of broader population. However, since only half of the patients are used for development or validation, and with the large number of potential biomarkers for consideration, a large sample size may be need to adequately power the trial.
Cross-validated adaptive signature design (Freidlin et al, 2010)[]11 is an extension of the adaptive signature design, which allows use of entire study population for signature development and validation.
Similar to the adaptive signature design, the initial null hypothesis is to test the benefit of the targeted therapy against the control is conducted in the overall population which is conducted at a slightly lower significance level α1 than the overall alpha α. The sensitive subset is determined by developing the classifier using the full population. It is done by the following steps.
- Test the initial null hypothesis of no treatment benefit in the overall population at α1, which is a slightly lower significance level than the overall α. If this hypothesis is rejected, then the targeted therapy is declared superior than the control treatment for the overall population and analysis is completed. If the first hypothesis is not rejected; then carrying out the following steps for signature development and validation.
- Split study population into “k” sub-samples.
- One of the “k” sub-samples is omitted to form a training sub-sample. Similar to the adaptive signature design, develop a model to predict the treatment difference between targeted therapy and control as a function of baseline covariates using training sub-sample. Apply the developed model to each subject not in this training sub-sample so as to classify patients as sensitive or non- sensitive.
- Repeat the same process leaving out a different sample from the “k” sub-samples to form training sub-sample. After “k” iterations, every patient in the trial will be classified as sensitive or non-sensitive.
- Compare the treatment difference within the subgroup of patients classified as sensitive using a test statistic (T). Generate the null distribution of T by permuting the two treatments and repeating the entire “k” iterations of the cross-validation process. Perform the test at α-α1. If the test is rejected, then the superiority is claimed for the targeted therapy in the sensitive subgroup.
The cross-validation approach can considerably enhance the performance of the adaptive signature design as it permits the maximization of information contributing to the development of the signature, particularly useful in the high-dimensional data setting where the sample size is limited. Cross-validation also maximizes the size of the sensitive patient subset used to validate the signature. One drawback is the fact that the signature for classifying sensitive patients in each subsample might not be the same and thus can cause difficulty in interpreting the results if a significant treatment effect is identified in the sensitive subgroup.
Zhou et al., (2008)[37] proposed an adaptive randomization method that allows the evaluation of treatments and biomarkers simultaneously. Using a Bayesian hierarchical framework, more patients are provided with potentially more effective treatments according to the patients’ marker profiles. Bayesian adaptive design can help to refine the estimation and randomization of the patients as the trial progresses.
The BAR enrichment design has been successfully implemented in a phase II Biomarker-integrated approaches of targeted therapy of lung cancer elimination (BATTLE) trial. The BATTLE project consists of one umbrella trial and four parallel phase II studies with biomarker-based targeted therapies in patients with advanced NSCLC previously treated with chemotherapy but subsequently failed. The main objective of the study was to estimate and test the disease control rate at 8 weeks for each treatment given patients’ tumor biomarker profiles. The Bayesian probit model was used to characterize the disease control rate for each treatment by marker subgroup with adaptive randomization.
One obvious limitation of the BAR design is adaptive randomization requires a quick turnaround time to learn from the interim data and adjust the randomization rate. As a result, the BAR design is applicable only for trials when the endpoint can be assessed in a relative short period of time.
Bayesian statistical methods are being used increasingly in clinical research because the Bayesian approach is ideally suited to adapting to information that accrues during a trial, potentially allowing for smaller more informative trials and for patients to receive better treatment. Bayesian design can provide an advantage over the non-Bayesian if certain conditions exist and have been the topic of a recent FDA guidance publication (2012). However, Korn and Freidlin (2011)[19] conducted simulations and pointed out that the Bayesian adaptive randomization designs are not necessarily more efficient than non-Bayesian designs. As for choosing beforehand the type of analysis to be used Bayesian or non-Bayesian, careful consideration based on the research purpose and the prior information for related studies is recommended.
We summarize the adaptive designs we reviewed above in the Table 2.
Discussion
In this paper, we gave an overview of biomarker-driven clinical trial designs utilizing predictive biomarker enrichment strategies that are growing in the statistical literature, with a focus on biomarker- driven adaptive designs so as to increase the power and efficiency to detect an effective therapy with regard to a predictive biomarker in clinical trial.
There are a number of issues one needs to consider before designing a trial with a predictive biomarker component [15]. First, we need to evaluate the strength of preclinical evidence for a potential predictive biomarker. If there is compelling preliminary evidence that the experimental therapy does not provide benefit to all the patients, and the benefit is restricted to a subset of patients expressing a molecular or genetic value, an enrichment strategy may be adopted. Otherwise, an unselected or all-comers strategy may be wise so that there is no missed opportunity. Second, we need to evaluate whether the prevalence of the biomarker positive group is high, moderate or low. If the prevalence is high, population enrichment may be redundant and a traditional design could render the greatest commercial value and market reach. Thirdly, as indicated by the FDA, the accuracy of the measurements used to identify the enrichment population and the sensitivity and specificity of the enrichment criterion in distinguishing responders and non-responders are also critical issues. When the assay is not 100% perfect to dichotomize patients to biomarker positive and negative groups, the efficiency of targeted clinical trials will be affected in a negative way. Let λsens denote the sensitivity of the assay for diagnosing marker+ patients and let λsens denote the corresponding specificity, then the treatment effect for the enrichment study will be diluted by:
If 2nT denote the number of patients randomized to the targeted trial, then 2nT/{(1-λspec) γ+ λsens(1-γ)} is the expected number of screened patients to enroll 2nT randomized patients.
Thus, the assay specificity is critical to determine the efficiency of targeted clinical trials with regard to required number of randomized patients while the assay sensitivity played a vital role with regards to required number of screened patients.
An accurate, reproducible and adequately validated assay is essential for establishing desired therapeutic activity and clinical validation of the biomarker (usually realized by a companion diagnostic kit from a central lab) in a prospective manner. In addition, the feasibility and timing to obtain a biopsy (de-novo or archived) or serum sample at baseline prior to randomization determines whether the biomarker can be prospectively validated.
Biomarkers are becoming increasingly important for streamlining drug discovery and development in the new era of precision medicine. Nowadays, many biomarkers are being used in phase III clinical studies and have helped in bringing forward effective treatments to marker-defined patient populations in a timely manner. A few examples include: use of HER2 expression in the study of Lapatinib plus letrozole for metastatic breast cancer; use of KRAS mutation status in the study of cetuximab plus chemotherapy for stage III colon cancer, use of EGFR expression in the study of erlotinib for metastatlic non-small cell lung cancer.
In addition to the case of predictive biomarker for identifying sensitive patient population, case of biomarkers that relate to early treatment selection [32] is also an importantresearch area but not covered in our paper.
References
- Baker SG, Kramer BS, Sargent DJ, Bonetti M (2012) Biomarkers, subgroup evaluation, and clinical trial design. Discov Med. 13(70): 187-192.
- Bayer R, Galea S (2015) Public Health in the Precision-Medicine Era. N Engl J Med. 373(6): 499-501.
- Beckman R, Clark J, Chen C (2011) Integrating predictive biomarkers and classifiers into oncology clinical development programmes. Nat Rev Drug Discov. 10(10): 735-748.
- Chang M (2006) Bayesian adaptive design method with biomarkers. ASA Pharmaceutical Report 14(2): 7-11.
- Chang M (2007) Adaptive Design Theory and Implementation Using SAS and R. Chapman & Hall/CRC, Taylor & Francis, UK.
- Chang M (2008) Biomarker Development, in Statistics for Translational Medicine. Taylor and Francis, UK.
- Chapman PB, Hauschild A, Robert C, Haanen JB, Ascierto P, et al., (2011) Improved survival with vemurafenib in melanoma with BRAF V600E mutation. N Engl J Med. 364(26): 2507-2516.
- Chow SC, Chang M, Pong A (2005) Statistical consideration of adaptive methods in clinical development. J Biopharm Stat. 15(4): 575–591.
- Chow SC, Chang M (2011) Adaptive design methods in clinical trials. (2nd Edn), CRC Press, UK.
- Collins FS, Varmus H (2015) A new initiative on precision medicine. N Engl J Med. 372(9): 793-795.
- Freidlin B, Jiang W, Simon R (2010) The cross-validated adaptive signature design. Clin Cancer Res. 16(2): 691-698.
- Gallo P, Chuang-Stein C, Dragalin V, Gaydos B, Krams M, et al., (2006) Adaptive design in clinical drug development – an executive summary of the PhRMA Working Group. J Biopharm Statistics. 16(3): 275–283.
- Graiger D (2016) The mutual benefits of rare disease research and precision medicine. journal of precision medicine.
- Hawgood S, Barnard IG, O’Brien TC, Yamamoto KR (2015) Precision medicine: Beyond. the inflection point. Sci Transl Med. 7( 300): 300-317.
- Huang B, Wang J, Menon S (2015) Population enrichment designs. Chapter 11. Modern . approaches to clinical trials using SAS: Classical, adaptive and Bayesian methods, edited by Sandeep Menon and Richard Zink. SAS Press.
- Jameson JL, Longo DL (2015) Precision Medicine — Personalized, Problematic, and Promising. N Engl J Med. 372(23): 2229-2234.
- Jenkins M, Stone A, Jennison C (2011) An adaptive seamless phase II/III design for oncology trials with subpopulation selection using correlated survival endpoints. Pharm Stat. 10(4): 347–356.
- Jiang, W, Freidlin B, Simon R (2007) Biomarker-adaptive threshold design: a procedure for evaluating treatment with possible biomarker-defined subset effect. J Natl Cancer Inst. 99(13): 1036-1043.
- Korn EL, Freidlin B (2011) Outcome-adaptive randomization: Is it useful?. J Clin Oncol. 29(6): 771-776.
- Mandrekar SJ, Sargent D (2009) Clinical trial designs for predictive biomarker validation: theoretical considerations and practical challenges. J Clin Oncol. 27(24): 4027-4034.
- Mirnezami R, Nicholson J, Darzi A (2012) Preparing for Precision Medicine. N Engl J Med. 366(6):491.
- Sargent DJ, Conley BA, Allegra C, Collete L (2005) Clinical trial designs for predictive marker validation in cancer treatment trials. J Clin Oncol. 23(9): 2020-2227.
- Shun Z, Lan KK, and Soo Y (2008) Interim treatment selection using the normal approximation approach in clinical trials. Stat Med. 27(4):597-618.
- Simon R (2010) Clinical trial designs for evaluating the medical utility of prognostic and predictive biomarkers in oncology. Per Med. 7(1): 33-47.
- Simon R, Maitournam A (2004) Evaluating the efficiency of targeted designs for randomized clinical trials. Clin Cancer Res. 10(20): 6759-6763.
- Simon N, Simon, R (2013) Adaptive Enrichment Designs for Clinical Trials.Biostatistics. 14(4):613-25.
- Simon R, Wang SJ (2006) Use of genomic signatures in therapeutics development in oncology and other diseases. Pharmacogenomics J. 6(3): 166-173.
- Song X, Pepe MS (2004) Evaluating markers for selecting a patient's treatment. Biometrics. 60(4): 874-883.
- Song Y, Chi GY (2007) A method for testing a prespecified subgroup in clinical trials. Stat Med. 26(19): 3535-3549.
- Wang J (2013) Biomarker informed adaptive design. PhD Desertation, Biostatistics, Boston University, Boston, MA.
- Wang J, Chang M, and Menon S (2014) Clinical and Statistical Considerations in Personalized Medicine; Biomarker-Informed Adaptive Design . Chapman and Hall/CRC, Taylor & Francis Group,New York. 129–148.
- Wang J, Chang M, Menon S (2015) Biomarker informed add-arm design for unimodal response. J Biopharm Stat. 26(4): 694-711.
- Wang SJ, O’Neill RT, Hung J (2007) Approaches to Evaluation of Treatment Effect in Randomised Clinical Trials with Genomic Subset. Pharmaceutical Statistics. 6(3), 227-244.
- Wang SJ, Hung J, O'Neill RT (2009) Adaptive patient enrichment designs in therapeutic trials. Biom J. 51(2): 358--374.
- Weir CJ, Walley RJ (2006) Statistical evaluation of biomarkers as surrogate endpoints: a literature review. Statist Med. 25(2):183--203.
- Woodcock J (2005) "FDA introduction comments: clinical studies design and evaluation issues". Clin Trials. 2(4): 273–275.
- Zhou X, Liu S, Kim ES, Herbst RS, Lee J (2008) Bayesian adaptive design for targeted therapy development in lung cancer—a step toward personalized medicine. Clin Trials. 5(3): 181-193.