Key Words

Natural Convection; Boundary Layer Flow; MHD Nanofluid; Heat and Mass Transfer; Porous Media.

Introduction

Porous media and heat and mass transfer phenomenon is an issue that has attracted the attention of many researchers from different branches of science. Due to the broad applications of porous medium in various fields of engineering including thermal insulation of buildings, catalytic chemical reactors, groundwater pollution, ceramic industry, biological technology, energy storage units, heat exchangers, cooling, electronics, oil and etc., it is essential to study basically how heat and mass transfer is in this media; because a comprehensive study is a means to improve engineering systems containing porous materials and enhancing their performance and quality. Different researches are conducted in last two decades in the field of porous media. Nakayama et al., [1] employed an integral solution for a non-Darcy natural convection flow on a vertical flat surface and a vertical cone in a saturated porous media. They observed that the heat transfer rate decreases with increasing the Grashof number; but the boundary layer thickness of dimensionless temperature is in direct relation to the Grashof number. Murthy and Singh [2] investigated heat and mass transfer on a vertical flat wall in a porous media. They observed that the boundary layer thickness of dimensionless temperature increases as the mass flux parameter reduces or by changing the suction mode to injection mode. They also concluded that when the mass flux of the surface increases, the Grashof number decreases, and also with increasing the buoyancy rate parameter, the rate of the dimensionless heat and mass transfer increases. Heat and mass transfer in the vicinity of a vertical wall for a non-Darcy natural convection flow in a porous media are studied by Wang et al., [3]. Based upon their results, when the Grashof number, Lewis number and buoyancy proportion are constant, the non-dimensional velocity, temperature and concentration increase with reducing the mass flux. They also illustrated that the dimensionless heat transfer in suction mode is more than other modes. El-Amin [4] explored the effect of dispersion on natural convection heat and mass transfer in a porous medium for Darcy and non-Darcy flow. He concluded that the dimensionless heat transfer in a Darcy flow is more than non-Darcy one. He also indicated that with an increment of the dispersion coefficient, the velocity boundary layer thickness decreases and the boundary layer thickness of dimensionless temperature increases. In a numerical study, Pal [5] investigated mixed convection heat transfer on a vertical heated wall in a porous media using Rung-Kutta method. He demonstrated that with an increase of Prandtl number and local inertia parameter, the dimensionless temperature and velocity profiles decrease.

Magnetohydrodynamic is a field of science studies the interaction effect of magnetic field and the fluid. In order to understand and study this field of science, knowing the governing equations of magnetic field and fluid flow and the effect of these on each other's is essential. Various researches [6-12] have been carried out in the field of magnetohydrodynamic in recent years. Pal [13] examined the effect of magnetic field on mixed convection heat transfer on a vertical heated surface in a porous medium with various porosity coefficients. He reported that the boundary layer thickness of dimensionless velocity increases when the magnetic field parameter and local inertia increase, while this behavior is reverse for boundary layer thickness of dimensionless temperature. Mahdy and Mohamed [14] conducted a numerical investigation to study the effect of magnetohydrodynamic on a non-Darcy natural convection flow in a porous media on a vertical wavy wall. They observed that with augmentation of the Grashof number and magnetohydrodynamic parameter, the boundary layer thickness of dimensionless velocity decreases and the boundary layer thickness of dimensionless temperature increases in a constant amplitude of wave. They also observed that by reducing the wave amplitude, the Grashof number and magnetohydrodynamic parameter, the Nusselt number augments. Natural convection heat and mass transfer on a vertical surface in a porous media under the influence of a magnetic field is studied by Kishan et al., [15]. They demonstrated that with increasing magnetic field strength, the dimensionless velocity profile decreases, while the dimensionless temperature profile increases near surface. Very recently, Mabood et al., [16] numerically investigated the MHD boundary layer flow and heat and mass transfer of a nanofluid using Rung-Kutta method. They illustrated that the dimensionless velocity decreases and temperature increases with magnetic parameter.

Nowadays, miniaturizing heat transfer systems and increasing heat flux in industrial applications necessitate optimizing heat transfer in devices such as computer chips. Nano technology has a great potential to increase heat transfer of systems in small volume. This means that by adding nanoparticles to the base fluid, it is possible to improve the thermo-physical properties of the fluid. As early as 1995, Choi [17] used the term "nanofluids" for suspensions of nanoparticles in a liquid and claimed that these fluids have many differences than common solid-liquid suspensions and macrofluids such as the preparation and properties of stability and transmission. In an analytical investigation, Hamad [18] examined the effect of nanoparticles on natural convection around a horizontal flat surface and in the presence of a magnetic field. He used nanoparticles such as Cu, Hg, Ti and Al2O3. He revealed that the dimensionless heat transfer has a reverse relation with volume fraction of nanoparticles and magnetohydrodynamic parameter. Uddin et al., [19] studied natural convection boundary layer flow over a horizontal heated flat plate in a porous media engulfed by nanofluid. They observed that with increasing the inertia rate, mass flux parameter and Brownian motion, the boundary layer thickness of dimensionless velocity increases. Rosca et al., [20] investigated a non-Darcy mixed convection flow on a horizontal wall in a saturated porous media. The wall temperature was considered variable and Cu, TiO2 and Al2O3 nanoparticles are used. They demonstrated that the dimensionless velocity profile near the wall decreases when the volume fraction of nanoparticles increases. Other researches in the field of using nanofluid are presented in [21-30].

As evidenced by comprehensive survey of literature which is mentioned above, it can be concluded that there is no any study which would be applied to the field of natural convection heat and mass transfer of MHD nanofluid in a porous media. Therefore, the objective of this study is to examine the effect of a magnetic field on laminar nan-Darcy natural convection of water-Al2O3 nanofluid in a porous media near a vertical flat wall. Concentration and temperature of the wall is constant and the temperature and concentration of the ambient is T∞ and C∞, respectively. This study is done for different values of the Nusselt numbers, Grashof numbers, Sherwood numbers, Lewis numbers, Soret numbers and Hartmann numbers. The effects of volume fraction of nanofluid and Buoyancy number on Nusselt number are also studied.

The geometry, governing equations and boundary conditions

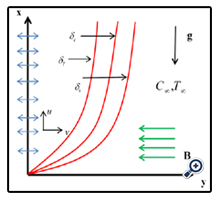
The geometry of the problem is shown in Figure 1. The constant temperature and concentration of the wall are Tw and Cw, respectively. And the wall is located in the vicinity of a porous medium containing water-Al2O3 nanofluid with temperature and concentration of T0 and C0, respectively. The wall could become permeable (Vw = 0) or impermeable (Vw ≠ 0). The volume forces are gravity and magnetic. The size of the effective magnetic field is constant and its direction is perpendicular to the wall. δv, δT and δv are the boundary layer thickness of velocity, temperature and concentration, respectively. Thermo-physical properties of water as a base fluid and Al2O3 nanoparticles are presented in Table 1.

The nanofluid electrical conductivity coefficient [32], density, heat capacity, volume expansion coefficient, diffusion coefficient, viscosity [33] and thermal conductivity [34] are obtained from the following relations, respectively:

×

Figure 1:

Close

Figure 1. Schematic of the problem.

×

Table 1:

Close

Table 1. Thermo-physical properties of base fluid (in temperature 300 K) and nanoparticles [31].

The effect of the magnetic field appears in the momentum equations as the Lorentz volume force F→ = J→ + B→ where the magnetic field is B→ and J→ is the circuit density [15]. The governing equations of the flow field including the continuity equation, momentum, energy and mass transfer equations inside the boundary layer and near the vertical flat wall in twodimensional Cartesian coordinate are [35, 36]:

along with the Boussinesq approximation,

By considering the boundary layer approximation and making use of Boussinesq approximation, the momentum equation becomes:

Here x and y are the Cartesian coordinates and u and v are the velocity along the x and y direction. T, P, βc and βTcf are the temperature, pressure, mass expansion coefficient and thermal expansion coefficient, respectively. cp and cs are the specific heat at constant pressure and concentration susceptibility. v is kinematic viscosity of the fluid. K, c, Dm, C and B0 are permeability of the porous medium, empirical constant, mass diffusion, concentration and magnetic field strength, respectively. vw can be expressed as follow:

in which E is a real constant. The boundary conditions are:

In order to solve the governing equations, the similarity solution is applied. The similarity parameters are defined as [37]:

The Hartmann number, modified Rayleigh number and Grashof number are defined as follows [2]:

In the above equations ƒ, ƒ',θ and Φ(η) and are the dimensionless stream function, vertical velocity, temperature and concentration. When these parameters are put in equations 11, 12 and 14, these equations change as follows:

where N (Buoyancy number), Df (Dufour number), Le (Lewis number) and Sr (Soret number) in above equations are defined as follows, respectively:

The new boundary conditions are:

In order to solve these equations, a fourth order Rung-Kutta method is applied. ƒw is the mass flux parameter [2]. ƒw > 0 corresponds to suction and ƒw > 0 corresponds to blowing or injection.

Dimensionless heat and mass transfer coefficient can be written as follows:

Results and Discussion

In this study, flow field and heat and mass transfer of water- Al2O3 nanofluid are investigated on a vertical flat wall in a porous media and in the presence of the magnetic field using similarity solution. The effect of parameter such as volume fraction of nanoparticles, Grashof number, Hartmann number, Lewis number, Soret number, Buoyancy number, Dufour number and mass flux parameter on Nusselt number and Sherwood number are examined. The study is done in Φ = 0 to φ = 0.06. There are three modes for the mass flux: suction mode (ƒw = +1), impermeable walls ( ƒw = 0 ) and blowing or injection mode (ƒw = -1). Values of the Grashof number are considered Gr = 0 and Gr = 1, and values of the Hartmann number are considered Ha = 0, Ha = 1, Ha = 2. Buoyancy number and Lewis number are in the variable range of N = 0-3.5 and Le =0-50, respectively. The Soret and Dufour numbers also are considered zero and one in each case.

Independence results from grid

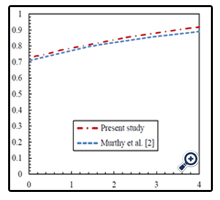
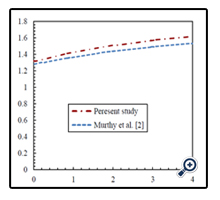
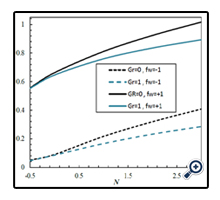
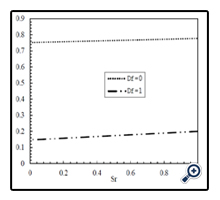
To verify the computer program results, Murthy et al., [2] solution geometry with our program is simulated. The results of the Nusselt number and Sherwood number in terms of the Buoyancy number are compared to their results in Figures 2 and 3. As can be seen and in the same condition, the relative discrepancy between the values obtained for the Nusselt number and the Sherwood number is negligible and ensures the modeling results accuracy.

×

Figure 2:

Close

Figure 2. Comparison of the Nusselt number in terms of Buoyancy number.

×

Figure 3:

Close

Figure 3. Comparison of the Sherwood number in terms of Buoyancy number.

Study of the effective parameters on flow, temperature and concentration field

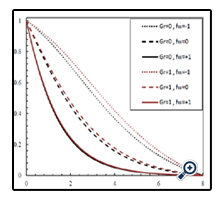
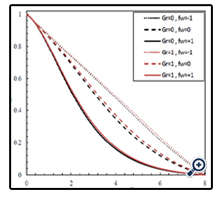
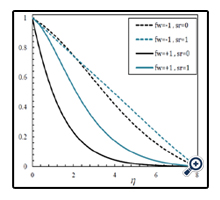
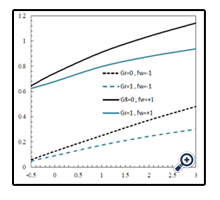
In Figures 4, 5 and 6, effect of the Grashof number on the velocity, temperature and concentration profiles are investigated in different mass fluxes and in φ = 0.01, N = 1, Df = 1, Sr = 1, Ha = 1 and Le = 1. In Figure 4, values of the velocity profile in adjacent areas of the wall are declined significantly and in farther areas decreases slightly. Also, when The Grash of number increases, the boundary layer thickness of the dimensionless velocity increases. In Figure 5, dimensionless temperature profile increases by increasing the Grash of number and thickness of the temperature boundary layer is almost increases, too. Actually, the Grash of number is a criterion for separation of the fluid through the porous wall and the higher values of the Grashof number signifies less inertia values, further separation and also a larger temperature boundary layer thickness. In addition, one of the effects of suction is enhancement of the friction coefficient of the porous wall compared to the impermeable wall. Because when the amount of fluid is pulled into the wall, the boundary layer becomes thinner. The opposite of this situation occurs when the fluid is injected to the wall. In Figure 6, concentration profile and thickness of the concentration boundary layer increases by increasing the Grashof number.

×

Figure 4:

Close

Figure 4. Variations of the velocity profile with Grashof number and mass flux.

×

Figure 5:

Close

Figure 5. Variations of the temperature profile with Grashof number and mass flux.

×

Figure 6:

Close

Figure 6. Variations of the concentration profile with Grashof number and mass flux.

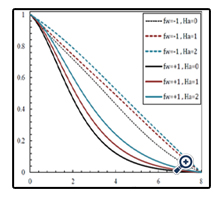
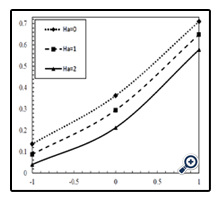
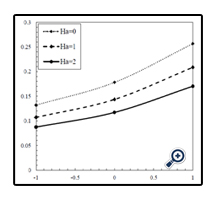
In Figure 7, 8 and 9, the effect of Hartmann number on the velocity, temperature and concentration profiles are illustrated in φ = 0.01, N = 1, Df = 1, Sr = 1, Le = 1 and Gr = 1 and in different values of mass fluxes. As can be seen in these Figures, when the intensity of magnetic field increases, velocity values near the wall or far from the wall decreases significantly. In addition, by increasing the Hartmann number, the velocity boundary layer thickness decreases in both suction and blowing modes. To put this in perspective, by increasing the Hartmann number, the Lorentz force also increases and this force changes the buoyancy force and eventually causes changing the intensity and thickness of the velocity boundary layer. This behavior is thoroughly in reverse for the temperature and concentration profiles which means that enhancement of the Hartmann number, causes an increase in the thickness of the temperature and concentration boundary layers.

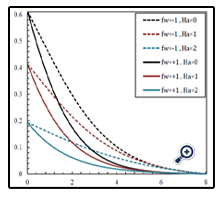
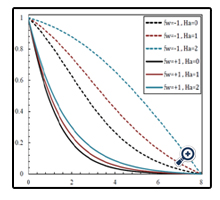
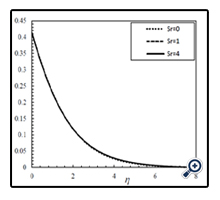
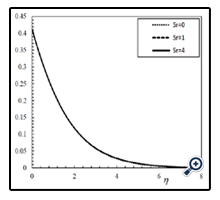
Figures 10 and 11 illustrate variations of velocity and temperature profile in terms of η in different Soret numbers and for φ = 0.01, N = 1, Df = 1, Ha = 1, Le = 1 and fw = +1. As can be seen in these Figures, changes in velocity and temperature profiles in Sr = 0 and Sr = 1 is negligible. But it is obvious in Figure 12 that by increasing Sorat number from zero to one at the same conditions, the concentration profile is changed significantly. For ƒw = -1, when the Soret number increases, concentration decreases in the vicinity of the wall and increases far from the wall. For ƒw = +1, on the other hand, in all of the spots, concentration and boundary layer thickness increases when the Soret number increases.

×

Figure 7:

Close

Figure 7. Variations of the velocity profile with Hartmann number and mass flux.

×

Figure 8:

Close

Figure 8. Variations of the temperature profile with Hartmann number and mass flux.

×

Figure 9:

Close

Figure 9. Variations of the concentration profile with Hartmann number and mass flux.

×

Figure 10:

Close

Figure 10. Variations of the velocity profile with Soret number.

×

Figure 11:

Close

Figure 11. Variations of the temperature profile with Soret number.

×

Figure 12:

Close

Figure 12. Variations of the concentration pr ofile with Soret number and mass flux.

Study of the effective parameters on Nusselt number

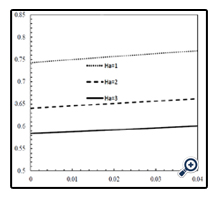
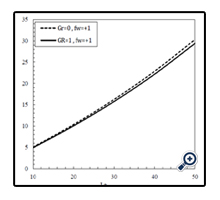
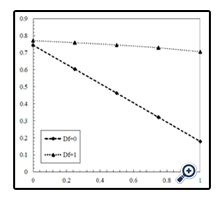
Figure 13 shows variations of the Nusselt number in terms of volume fraction of nanoparticles in different Hartmann numbers and for N = 1, Df = 1, Sr = 1, Le = 1 and ƒw = +1. As expected, the Nusselt number increases when the volume fraction of nanoparticles increases. In Figure 14, effect of the Buoyancy number on the Nusselt number is shown in different Grashof numbers and mass flux parameters and for φ = 0.01, Df = 1, Sr = 1, Le = 1 and Ha = 1. As can be seen in this Figure, by increasing the Buoyancy number, the Nusselt number increases in both suction and blowing modes. Also, in suction mode (ƒw = +1), the Nusselt number is more than blowing mode. Because in suction, the boundary layer thickness is thinner than blowing and the boundary layer is more influenced by the wall temperature and thus the Nusselt number increases. Furthermore, by increasing the Grash of number from zero to one, the heat transfer coefficient decreases in both suction and blowing modes. In fact, in natural convection, the average velocity of the fluid increases when the Grashof number increases in which results reducing the contact time between fluid and wall and thus, reduces the heat transfer and the Nusselt number. It should be noted that this does not reduce the rate of heat transfer. Because when the Grash of number increases, more fluids are affected by the wall temperature. Even though the average temperature of the fluid decreases slightly, this reduction will be compensated by increasing the flow rate that can increase the heat transfer. In Figure 15, variations of the Nusselt number in terms of the mass flux is indicated in different Hartmann numbers and for φ = 0.01, N = 1, Df = 1, Sr = 1, Le = 1 and Gr = 1. According to this Figure, The Nusselt number increases when the Hartmann number decreases. Because by increasing the magnetic field due to increasing the Lorentz force, the buoyancy force increases too. In Figure 16, variations of the Nusselt number in terms of the Lewis number is indicated in different Grashof numbers and for φ = 0.01, N = 1, Df = 1, Sr = 1, fw = +1 and Ha = 1. It is observed that by increasing the Lewis number, the heat transfer coefficient decreases. Figure 17 indicates variations of the Nusselt number in terms of the Soret number in Dufour number of zero and one and for φ = 0.01, N = 1, fw = +1, Le = 1, Ha = 1 and Gr = 1. With augmentation of the Soret number, the temperature gradient increases and thus, the heat transfer coefficient increases too. Furthermore, by increasing the Dufour number, the heat transfer coefficient reduces. In fact, when the Dufour number increases, the temperature gradient inside the boundary layer reduces and as a result, the heat transfer coefficient decreases.

×

Figure 13:

Close

Figure 13. Variations of the Nusselt number in terms of volume fraction in different Hartmann numbers.

×

Figure 14:

Close

Figure 14. Variations of the Nusselt number in terms of Buoyancy number in different Grashof numbers and mass fluxs.

×

Figure 15:

Close

Figure 15. Variations of the Nusselt number in terms of mass flux in different Hartmann numbers.

×

Figure 16:

Close

Figure 16. Variations of the Nusselt number in terms of Lewis number in different Grashof numbers and mass fluxs.

×

Figure 17:

Close

Figure 17. Variations of the Nusselt number in terms of Soret number in different Dofour numbers.

Study of the effective parameters on Sherwood number

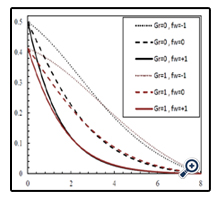
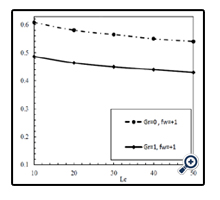
In Figure 18, effect of the Buoyancy number on the mass transfer coefficient is shown in Gr = 0.1 and for φ = 0.01, Df = 1, Sr = 1, Le = 1, fw = ± 1, Ha = 1. When the Buoyancy number increases, concentration gradient inside the boundary layer augments and as a result, the mass transfer coefficient increases in suction and blowing modes. Figure 19 illustrates the effect of magnetic field on mass transfer in different mass fluxes and for φ = 0.01, N = 1, Df = 1, Sr = 1, Gr = 1, and Le = 1. As can be seen, presence of the magnetic field decreases the mass transfer coefficient. Also, when the mass flux increases and alters from blowing to suction, the boundary layer thickness of concentration decreases and concentration gradient inside the boundary layer increases and thus the Sherwood number augments. In Figure 20, the variations of the Sherwood number in terms of the Lewis number is indicated in Gr = 0.1 and for φ = 0.01, N = 1, Df = 1, Sr = 1, fw = +1 and Ha = 1. It is obvious that by increasing the Lewis number, the Sherwood number augments too. In Figure 21, the variations of the Sherwood number in terms of the Soret number is illustrated in Df = 0.1 and for φ = 0.01, N = 1, Le = 1, fw = +1, Gr = 1, Ha = 1. By increasing the Dufour number, the concentration gradient inside the boundary layer increases. Therefore, the mass transfer coefficient increases too. Also, with augmentation of the Soret number, the Sherwood number decreases.

×

Figure 18:

Close

Figure 18. Variations of the Sherwood number in terms of Buoyancy number in different Grashof numbers and mass fluxs.

×

Figure 19:

Close

Figure 19. Variations of the Sherwood number in terms of mass flux in different Hartmann numbers.

×

Figure 20:

Close

Figure 20. Variations of the Sherwood number in terms of Lewis number in different Grashof numbers.

×

Figure 21:

Close

Figure 21. Variations of the Sherwood number in terms of Soret number in different Dofour numbers.

Conclusion

In this study, the flow field and heat and mass transfer of natural convection of water-Al2O3 nanofluid is investigated near a vertical surface and in a porous medium and in the presence of a constant magnetic field. The flow is laminar, incompressible and non-Darcy, and water and nanoparticles are in thermal and concentration equilibrium. The governing equations that are Partial Differential Equations (PDEs) are changed into Ordinary Differential Equations (ODEs) with the aim of similarity parameters. The effect of different parameters such as Hartmann number, Grashof number, Nusselt number and etc. on flow field and heat and mass transfer are examined. According to the obtained results it is obvious that:

1. When the Grashof number increases, the Nusselt number decreases in both suction and blowing.
2. By increasing the Hartmann number, the Nusselt number and Sherwood number decrease.
3. When the Dufour number increases, the temperature gradient decreases and concentration gradient augments inside the boundary layer. Consequently, the Nusselt number decreases and the Sherwood number increases.
4. Increasing of the Buoyancy number causes increasing the concentration gradient and temperature gradient. Therefore, the Nusselt number and the Sherwood number increases.
5. With an increase of the Lewis number and Soret number, the mass transfer coefficient augments and reduces, respectively.
6. Heat and mass transfer in a porous medium in suction mode (fw > 0) is more than blowing mode (fw < 0 ) and impermeable mode (fw = 0). So, in order to increase heat and mass transfer, the suction mode is a suitable choice.

List of Symbols

B0   :   Magnetic field intensity
cp   :   Specific heat at constant pressure (Jkg-1K-1)
E   :   Electrical field
ƒ   :   Dimensionless stream function
ƒw   :   Mass flux
Gr   :   Grashof number
g   :   Gravity acceleration
Ha   :   Hartmann number
h   :   Heat transfer coefficient
J   :   Circuit density
K   :   Impermeability coefficient
κ   :   Thermal conductivity coefficient
Nu   :   Nusselt number
P   :   Pressure (Pa)
Sr   :   Soret number
Df   :   Dufour number
Ra   :   Rayleigh number
Le   :   Lewis number
N   :   Buoyancy number
Re   :   Reynolds number
T   :   Temperature (K)
u, v   :   Velocity components in x and y direction
x   :   Horizontal axes coordinate
y   :   Vertical axes coordinate

Greek symbols

η : Similarity variable
µ : Dynamic viscosity
α : Thermal diffusity
ρ : Density(kgm-3)
ν : Kinematic viscosity
φ : Nanoparticle volume fraction
Ψ : Stream function(m2s-1)
σ : Electrical conductivity coefficient

Subscripts

ƒ : Fluid
nƒ : Nanofluid
w : Wall

Acknowledgment

The authors wish to thank the Energy Research Institute of the University of Kashan for their support regarding this research (grant no. 65473).