Multiscale Modeling for Material Phase Change Problems

International Journal of Nano Studies & Technology (IJNST) IJNST-2167-8685-05-001e

Multiscale Modeling for Material Phase Change Problems

Xiao S1*, Ni J1, Zhang Y2

1 The Department of Mechanical and Industrial Engineering, The University of Iowa, Iowa City, USA.
2 SMIT Center, School of Mechatronics Engineering and Automation, Shanghai University, Shanghai, China.

*Corresponding Author

Shaoping Xiao,
The Department of Mechanical and Industrial Engineering,
The University of Iowa, Iowa City, USA 52242.
E-mail: shaoping-xiao@uiowa.edu

Received: March 01, 2016; Published: March 02, 2016;

Citation: Xiao S, Ni J, Zhang Y (2016) Multiscale Modeling for Material Phase Change Problems. Int J Nano Stud Technol. 5(1e), 1-3. DOI : dx.doi.org/10.19070/2167-8685-160008e

Copyright: Xiao S© 2016. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.

A phase change is the transformation of a material from one phase or state of matter to another. It includes phase changes between solid, liquid and gaseous states of matter. Phase change problems, including melting and solidification, are very important in many engineering applications such as food freezing, metal processing, and solidification of castings. Numerical modeling has been one of important tools to study physical phenomena in phase change problems at various scales. Initially, the material phase change problems were studied at the macroscale, and the thermal diffusion equation was usually employed as one of governing equations:

where T is the temperature field and α is the thermal diffusivity.

The fixed grid methods [1-5], including both finite element methods (FEM) and finite difference methods (FDM), were employed to model and simulate material phase change problems by solving the governing equations numerically. The major advantage of fixed grid methods is that the methods can handle multi-dimensional problems efficiently. However, the fixed grid methods may sometimes be unstable when the phase interface moves at a distance larger than the spatial increment in one time step. The extended finite element method (XFEM) [6, 7] has been used to overcome the above issue raised in most fixed grid methods. The basic idea is to explicitly track the phase interface and to construct enriched elements depending on the interface position while keeping the fixed meshes. Therefore, the approximation can present the phase interface and the associated discontinuity in the temperature gradient within an element. Another alternative solution is to employ the variable grid methods [8, 9]. In the variable grid methods, either the space or time domain is divided into equal intervals, and the corresponding grid interval in the other domain is determined.

To study material change problems at the microscale, a thermal wave model [10] shall be employed:

where τ is the relaxation time. Li [11] compared the solutions of the thermal diffusion equation with those of the thermal wave equation for a heat transfer problem. It showed that the latter would clearly elucidate non-Fourier heat conduction behavior when the relaxation time of material could not be neglected at the microscale. Various approaches have been proposed to determine the relaxation time for the heat wave model due to phonon transport [12] or electronic transport [13]. Another approach could be using molecular dynamics (MD) simulation to calculate the relaxation time. Indeed, other thermal properties, including thermal diffusivity and latent heat, can also be determined via MD simulations. Those parameters can be passed to the governing equations of the material phase change problems at the microscale. This is socalled hierarchical multiscale modeling.

MD is also a powerful tool to understand the mechanism of material phase change at the nanoscale. In MD simulation, classical Lagrangian mechanics is employed. The atoms are modeled as particles, and the interactions between atoms are described by the empirical potential functions. Newtonian equations of motion are solved to update atomic velocities and positions. Rose and Berry [14] performed MD simulations of the melting process of a KCl cluster composed of 64 ions. Luo et al. [15] conducted MD simulations to investigate nonequilibrium melting and crystallization of the Lennard-Jones system, and evaluated serval interfacial kinematic parameters.

We studied ice melting [16, 17] as an example to demonstrate numerical modeling and simulation of material phase change problems at different scales as discussed in the above. We first conducted MD simulations using SPC/E ice model, and found that the ice melting speed was very fast at the beginning and then decreased with time at the nanoscale. To simulate the ice melting at the microscale, the heat wave equation and the equation for releasing latent heat of transformation at the phase interface were solved via FEM. The relaxation time of ice in the thermal wave model was calculated from MD simulations and compared well with the experimental data [18]. At the macroscale, the thermal diffusion equation was employed to investigate ice melting speed.

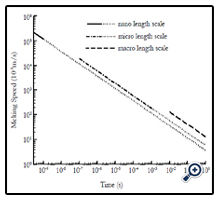
Figure 1 shows ice melting speeds at various scales. It should be noted that not only various length scales but also the corresponding time scales were considered. In addition, the dot lines represent the predicted ice melting speeds at the nano and micro length scales with larger time scales. Figure 1 clearly shows that melting speed at the nano length/time scale is much faster than those at the microscale and macroscale. Furthermore, ice melting speeds decrease with time evolution. If only considering various length scales, the ice melting speed at the nano length scale decreases with time. At the micro time scale, it is slower than the melting speed at the micro length scale. Similarly, at the macro time scale, the melting speeds at the micro and nano length scales are slower than the one at the macro length scale. The results illustrate that the ice melting speed is scale dependent.

Figure 1. Ice melting speeds at various scales.

Another approach to study material phase change problems at the microscale is the phase-field method, which was first introduced by Fix [19] and Langer [20], and has been experienced a growing interest in solidification and other areas. Caginalp and Fife [21] introduced surface tension and other important interfacial parameters in the phase-field model. They found that the classical phase change problems (sharp interface problems) could be recovered mathematically by using the phase-field approach. It could smooth the solution over a thin interface with a finite interfacial thickness, in which effects of surface tension and supercooling were included. In addition, Penrose and Fife [22] derived a thermodynamically consistent phase-field model. Wang and co-workers [23] presented this model based on the first and second thermal dynamics laws. An overview of the phase-field method for material phase change problems can be found in Boettinger's article [24].

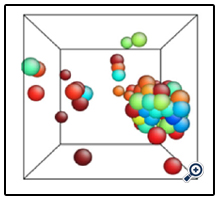
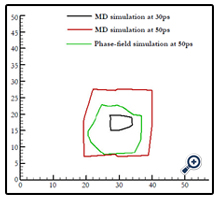
Here, we propose another hierarchical multiscale modeling to enhance the phase-field method in simulating material solidification problems. In this multiscale modeling, MD simulations are conducted at the nanoscale to investigation nucleation. The nucleus shape then is passed to the phasefield method as the input to initiate the microscale simulation. This multiscale modeling and simulation was demonstrated by studying copper crystallization. The embedded-atom method (EAM) potential was employed to conduct MD simulation of copper crystallization at the supercooling temperature of 850K. The system contained 4000 atoms subjected to periodic boundary conditions. It was found that crystallization occurred at 20ps with a few randomly located nuclei. One of them grew faster and became a cluster at 30ps, as shown in Figure 2. This largest cluster was mapped to a two-dimensional phase-field domain as the initial solid state configuration to initiate the microscale simulation. It shall be noted that the thermal properties and interfacial parameters were also obtained from MD simulations and were passed to the phase-field method. Those parameters include thermal diffusion coefficient, latent heat, relaxation time, interfacial thickness, interfacial energy and the anisotropy coefficients. The nucleus growth configurations from both phase-field method and MD simulation at 50ps are shown in Figure 3. The difference between two configurations are because MD simulations were three-dimensional while the phase-field simulation was twodimensional. In addition, the periodic boundary conditions were used in MD simulations but not in the phase-field simulation.

Figure 2. Solid cooper atoms during crystallization at 30ps.

In this paper, we discussed numerical modeling and simulation of material phase change problems at macroscale, microscale and nanoscale. Two hierarchical multiscale models were proposed. In the first model, the parameters in the thermal wave equation at the microscale were calculated via MD simulations. In the second one, MD simulation provided the nucleus configuration to initiate the phase-field simulation at the microscale. Studies of Ice melting and copper crystallization have been carried out to demonstrate the proposed multiscale models. They can be viewed as the frameworks to model and simulate material phase change problems.