Key Words

Nanoparticle; Crystallization; Molecular Dynamics; Amorphous Iron.

Introduction

Molecular dynamics simulation is an effective tool for gaining insight into the structure and dynamics of supercooled liquids and glasses, and it is also a very useful extension of experimental and analytical investigations in many fields of physics [1]. Especially, MD simulations have contributed to understanding of atomistic behavior of the solidification and melting of materials [2-6], since it is difficult to trace the motion of atoms directly by experiments. The crystalline mechanism of amorphous materials is also one of the problems studied by MD simulation. The crystallization proceeds when small crystalline regions are arised from the structural fluctuation in the amorphous solid. If the nuclei are larger than critical size, they will grow at the expense of noncrystalline part; otherwise they regress to the amorphous solid. Although there are intensive studies of crystal nucleation and growth [7-12], our knowledge about the dynamics and structure during these processes is still limited. Moreover, the correct description at atomistic level for the growth of crystalline phase in amorphous matrix is also unclear.

Recently, interest in nanoparticles has increased strongly in studying their unique properties [13-17]. For example, amorphous iron and iron-based nanoparticles exhibit specific magnetic, optical, sorption and other properties, and so this may leads to their advanced application in nanotechnology. Generally, amorphous state of nanoparticles is unstable and it can transform the crystalline state by using an appropriate annealing schedule.The stability of amorphous nanoparticles (ANP) against crystallization is of great interest, because this is related to their working ability in practice. The crystallization of ANP is studied mainly by experiments [18-24]. It was revealed that the glass and crystallization temperature of ANP is dependent on size. Also, the preparation conditions of ANPs influence on their transformation from amorphous to crystalline state. However, the crystalline mechanism of ANPs remains unclear. In particular, there is no information at atomistic level related to this problem. Therefore, this motivates the present study of the crystalline ANP by means of MD simulation.

Calculation Procedure

The MD simulation is conducted in a system containing 104 atoms Fe under free boundary conditions. The interactions between atoms are calculated with the Pak-Doyama potentials [5]. Initially, all atoms are randomly placed in a sphere with radii of 34 Å. Then the statistical relaxation is carried out until the system reaches the equilibrium. This sample is heated to temperature of 300 K. Then the sample is relaxed isothermally by 2.5×107 steps to obtain a well-equilibrated sample which is called 300-sample. In order to study a crystalline process we have prepared the second sample (900-sample) by heating 300-sample to 900 K and then relaxing isothermally over 107 steps.

To determine a particular atom is in a locally crystalline or amorphous environment one can apply Honeycutt- Andersenthe technique [25]. Accordingly, the structure is analyzed by pairs of atoms via four indexes: (i) the first index indicates whether or not they are near-neighbors; We use a fix cutoff radius to determine the near-neighbors Rcutoff= 3.35 Å. (ii) the second index equals to the number of near-neighbors they have in common; (iii) the third index equals to the number of bonds among common near-neighbors; (iv) the fourth index is related to arrangement of bonds among common near-neighbors. The 1661 and 1441 pairs are the characteristic pairs for a bcc crystal. Because the Honeycutt - Andersen the technique consumes long computing time, we apply it only to check some configurations during annealing process. We use a following technique. Each atom in the bcc lattice is surrounding by 14 neighboring atoms. Among them six ones have 4 neighbors and eight others have 6 neighbors in common with the central atom. This criterion is used to determine whether a particular atom is in a locally crystalline or amorphous environment. We define a set of such atoms including a central atom and 14 neighbors as a basic nucleus. During the crystallization we detect all basic nuclei and then determine a crystal cluster. There are three types of atoms. The first one is the atom belonging to amorphous phase. The second type relates the atom that is in the boundary between amorphous and crystal phases. We call this type AC-atom. The third type (Cr-atom) is the atom in the locally crystalline environment. Obviously, the crystal cluster contains AC-atoms and Cr-atoms. The atoms belonging to the crystal cluster is called CC-atoms.

Results and Discussion

The pair radial distribution function (PRDF) of bulk sample is defined as: g(r) = n(r)/4πr2drρ0     (1)

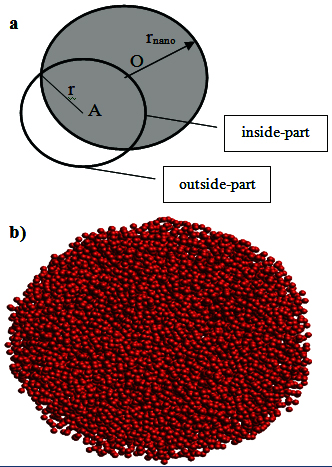
where n(r) is the number of atoms in a spherical shell with thickness dr at a distance r from another atom; ρ0 is the number density of the sample. For the spherical nanoparticle the function gnano(r) is determined as follows: For each atom we find all atoms in a spherical shell with thickness dr at a distance r from the central atom, this spherical shell consists of two parts which are the inside and the outside of the nanoparticle (see Figure 1a).

---

---

The function gnano(r) is defined as: gnano(r) = <nnano (r)>/<Vin>ρ0nano      (2)

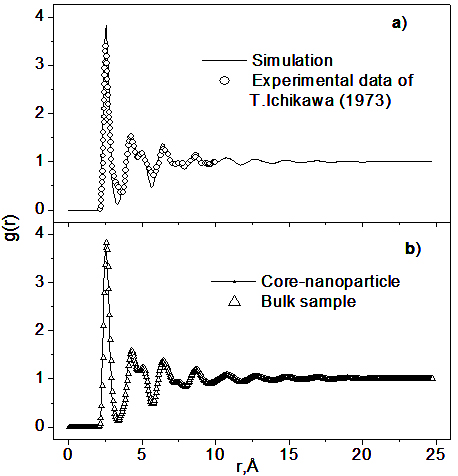
where the bracket <> means the averaging over different atoms in the nanoparticle; ρ0nano is the number density of nanoparticle; Vin and Vout are the volume of inside - and outside - part, respectively; Vin+Vout = 4πr2dr. The snapshot of 300-sample plotted in Figure 1b indicates a spherical shape of constructed sample. Its radius is 32.5 Å, and the sample consists of two parts: the surface and core. If all particles of the surface are removed, then we obtain a corenanoparticle with radii of 28 Å. The PRDF of bulk sample is used to clarify the structure of the core of nanoparticle. The PRDF of bulk sample is shown in Figure 2 together with experimental data and gnano(r) of the core-nanoparticle. The result indicates the similarity between structures of core-nanoparticle and bulk sample.

---

---

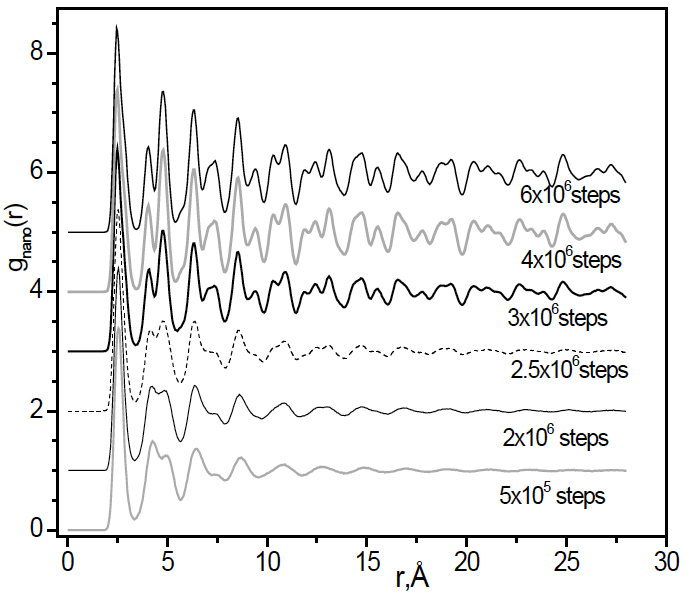
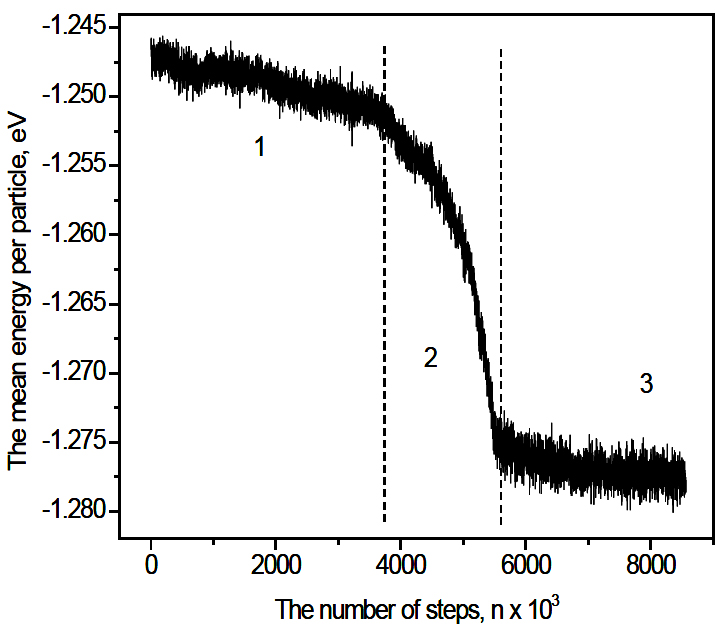
Figure 3 shows gnano(r) of 900-sample for different annealing time. For the short time the curve is similar to one of 300-sample samples. During this period the structure remains amorphous and no nucleation happens. For longer times, a number of new acute peaks appear showing distinct crystal characteristics. This evidences the structural transformation from amorphous to crystalline state. The phase change is related to the crystallization of material can be seen also from the evolution of the potential energy. As shown from Figure 4, the process can be divided into three periods. For the first period (n <3.8×106) the energy exhibits a subtle change corresponding to the formation of small nuclei and slow growth of crystal phase. In the second period (3.8×106 <n <5.8×106) there is a sharp drop in the energy which indicates a rapid growth of the crystalline phase. In the third period the energy fluctuates and the crystal cluster grows to a maximal size.

---

---

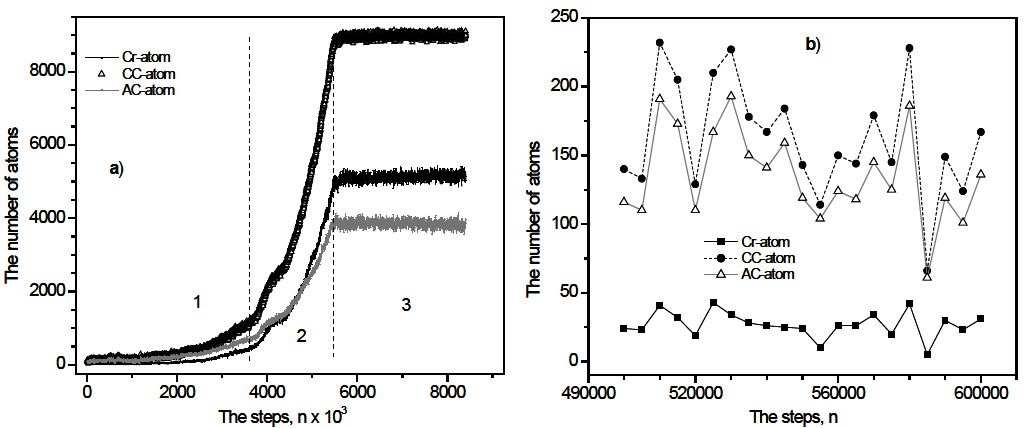
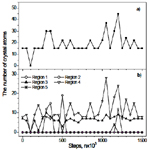
The nucleation and growth of crystal phase can be observed directly by the size of crystal cluster which is defined by the number of CC-atoms, AC-atoms and Cr-atoms. In Figure 5 we show the number of these types of atoms during annealing process. It shows three periods like the ones presented in Figure 4. In the first period the crystal cluster grows slightly, meanwhile for the second period the number of different types of atoms varies strongly. This demonstrates that if the size of crystal cluster is bigger than some critical value, then the crystal cluster grows rapidly to a maximal size. The critical size can be determined by the point in Figure 5a where a rapid growth is observed. This size is found to be 250-300 atoms. In the third period the number of all types of atoms fluctuates. The crystal cluster grows to a maximal size. For more detailed visualization the result for the period from 5×105 to 6×105 steps is plotted in Figure 5b.

---

---

---

---

One can see that the size of crystal cluster fluctuates from time to time. This implies that there are two opposite processes: the growth and the reduction of crystal cluster. The new basic nucleus may form inside the amorphous phase or in the boundary area between amorphous and crystal phases. During annealing process we determine the way by which the formation of new basic nucleus proceeds. The result shows that if the size of crystal cluster is bigger than 50 atoms, the formation of new basic nucleus is performed only by the second way.

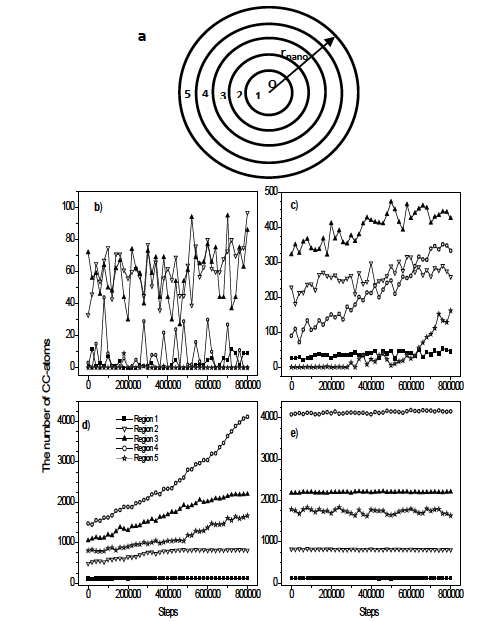
To examine how the crystal cluster grows inside the amorphous matrix we divide the sample into five regions which are schematically illustrated in Figure 6a. Here the region 1 is a sphere with radius of 6.9 Å. Remaining region is a spherical layer with thickness of 6.9 Å.

---

---

In Figure 6 we show the variation of different types of atoms during 8×105 steps at four moments of annealing process. In first period (Figure 6b), a crystal cluster consisting about 100 atoms spreads in the area between regions 2 and 3. Although the growth and reduction of crystal phase proceeds intensively in regions 2, 3 and 4, but the crystal cluster tends to grow forward to the center of the sample. For the next period (Figure 6c), the growth of crystal phase occurs in all regions, but the fastest ones happen in the region 4 and 5. At the end of the third period (Figure 6d) all atoms in regions 1, 2 and 3 belong to the crystal cluster, i.e. the core of the sample fully crystallizes. In the fourth period (Figure 6e) the crystal cluster spreads over whole the region 4, and the number of CC-atoms in the region 5 fluctuates. It implies that when the crystallization is complete, the sample consists of a core with crystalline structure and a surface with amorphous structure.

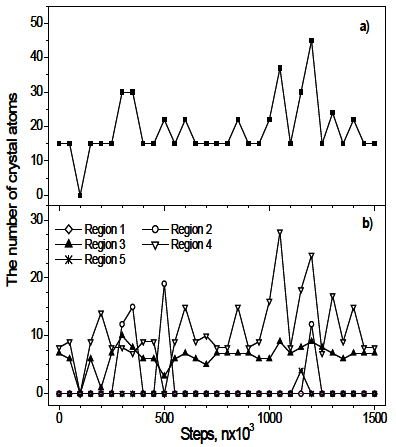
The 300-sample is annealed for long time (about 2.5×107 steps), however, the crystallization is not observed. Figure 7 shows the evolution of the crystal cluster for this sample. One can see that a crystal cluster consisting of several basic nuclei forms in the region 4, and sometime it grows up spreading to the region 3. However, the size of the nuclei (less than 50 atoms) is small and fluctuates. This implies that the thermal fluctuation at 300 K creates small nuclei, but they can not grow to a large size.

---

---

Conclusion

In this paper, the evolution of structural and thermodynamics properties of iron nanoparticle has been investigated by method of MD simulation. The nucleation and growth mechanism is studied by tracing crystal basic nuclei during annealing process. We found that the crystallization is observed when the sample is annealed for long times at 900 K. The phase of changing crystalline state is evidenced through the variation in PRDF and the mean potential energy. The result shows that the annealed sample transforms from amorphous to the bcc crystalline structure. The critical size of crystalline cluster is found to be 250-300 atoms. Final crystallized sample consists of two parts: a core with crystalline structure and a surface with amorphous structure. The nucleation doesn’t happen randomly in the sample, but intensively in a middle spherical layer. After that the crystal cluster grows firstly forward the center of the sample, and then spreads to the surface area. In this case when the sample is annealed at 300 K, a crystal cluster consisting of several basic nuclei has been detected in the area nearby to the surface of the sample. However, these nuclei cannot grow to a large size and the structure of nanoparticle remains amorphous.

Acknowledgement

The authors are grateful for support by the NAFOSTED Vietnam (grant No 103.01-2011.32) and technical support from the computing center of Hanoi Education University.