Analytical Solutions for the Point Source Spherical Blast Wave Propagation with γ = 7
Takahashi S
Tokyo Denki University, Hatoyama, Saitama, Japan.
*Corresponding Author
Shuji Takahashi,
Tokyo Denki University,
Hatoyama, Saitama, 350-0394, Japan.
E-mail: shuta@mail.dendai.ac.jp,
Article Type: Research Article
Received: February 27, 2015; Accepted: March 19, 2015; Published: March 20, 2015
Citation: Takahashi S (2015) Analytical Solutions for the Point Source Spherical Blast Wave Propagation with γ =7. Int J Aeronautics Aerospace Res. 2(1), 21-26. doi: dx.doi.org/10.19070/2470-4415-150003
Copyright: Takahashi S© 2015 This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.
Abstract
We consider the existence of a solution for the point-source spherical blast wave propagation caused by instantaneous explosion in case the ratio γ of the specific heats of the gas is 7. No similarity solutions of the Euler equations satisfy the conservation law on the shock front, so far as the atmospheric pressure ahead of the shock is not negligible. To describe the initial state, it can be used that the total amount of energy carried by the blast wave is constant and we use the condition of zero gas velocity at the center. By a hodograph transform this free boundary problem is converted into an eigenvalueThe problem for a system defined on a bounded rectangle such that this initial state assumption is satisfied. The solution is prescribed in the form of a power series expansion in one of the variables y = c2/u2 for front shock speed u and sound velocity c. Its convergence is shown by applying the fixed point theory of contractive mapping defined through linearization of the system. Our solution is local in y and exact there.
2.Introduction
3.Transformation
4.Main Theorem
3.1 Series Expansion
3.2 Local Existence
4.Solution For The Transformed System
4.1 Fundamental Solution
4.2 Assignment of Eigenvalue
5.Estimates for the Solution
5.1 Estimates for Λn
5.2 Estimates for Xn
5.3 Estimates for X'n
6.Conclusions
7.Acknowledgments
8.References
Keywords
CubeSat, Composite Materials, Finite Element Analysis, Modal Survey
Introduction
The Taylor-Sedov-Neumann (TSN) self-similar solution for atomic explosion [7] is an ap-proximate solution of a gas dynamics equations system to represent blast wave propagation from a point source explosion. The point source blast wave theory [4] is to provide in extending it to have its solution for wider applicability in PDE system:
T X = 0 ---------(1.1)
to the variable X and the parameters (α, γ) where α = 0, 1, 2 is the space dimension minus one and γ is the ratio of specific heats with 1 < γ < 10; X = {f(x, y), g(x, y), h(x, y), λ(y)} with f, g, h and λ corresponding respectively to the velocity, the pressure, the density and the decrement rate of propagation velocity; and x, y are given by x=r/R,y = c2/u2 with the radial coordinate r; R, U and Crespectvely the radius of the front shock wave, its veloocity and the sound velocity of free air, so that 0 ≤ x, y ≤ 1. These are supplemented by the Rankine-Hugoniot shock condition.
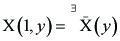 ------(1.2)
------(1.2)
and the condition that
f (0, y) = 0,------ (1.3)
which corresponds to that the velocity is zero at the center of explosion.
Formal expansion solution ([4]) of the above system as:
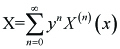 ------(1.4)
------(1.4)
can be determined successively starting from the TSN solution: X(0) (x) by substituting the above expression to Eq. (1.1) and using the conditions (1.2) and (1.3).
Approximate solutions with a few beginning terms of (1.4) have been utilized widely for various applications [4, 1] such as for blast wave from ordinary explosions, hypersonic flow problems, and so on, in promoting to have better approximation by adding more terms in the series of (1.4). In fact, they have been found as high as n = 6. These, together with pure mathematical interest arise naturally the question of convergence of the series to the existence of the solution [5, 3]. In [3] it is proved that the series in Eq. (1.4) converges for y ≤ y¯ for a certain small y¯, and the limit function is a solution of the system given by (1.1), (1.2) and (1.3).
Its process: a Banach space is introduced in the form of convergent series expansion as in Eq. (1.4) and the system is converted into the one which determines a mapping in this space ; the mapping is then shown to have the property of contraction in a closed ball in the space for y ≤ y¯ and the existence of a fixed point in the ball, hence the existence of the solution of the original system for y ≤ y¯ follows immidiately. In this process, the part to estimate the solution X(n) (x) for general n is the most hard since X(n) (x) is not prescribed exactly if (α, γ) ≠ (2, 7). (In [3] the approximate solution is prescribed with fuction ξn in [(5.17), 3], but ξn is not exactly given.)
In this connection, we consider here the special case of α = 2, γ = 7 (see [2]), to which X(0) (x) becomes simple to give, and the equation to determine X(n) (x), after appropriate transformations can be reduced to an ODE of constant coefficients, so that the determination of X(n)(x) in compliance with the conditions of (1.3), (1.4) is almost straight forward and X(n) (x) is given exactly.
Transformation
Our problem is prescribed as
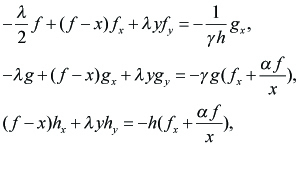 ----(2.1)
----(2.1)
for (x, y) ε (0, 1) × (0, 1) with the boundary condition
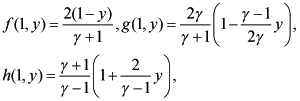 ---(2.2)
---(2.2)
with the initial condition
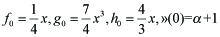 --(2.3)
--(2.3)
and with condition
f (0, y) = 0.---(2.4)
Here (2.3) is the similarity solution for (α, γ) = (2, 7). This is an eigenvalue problem such that eigenvalue λ(y) must be assigned so as to satisfy (2.4). (See [3] for the details.)
We transform the unknown functions (f, g, h, λ) to (Φ, ψ, χ, Λ) by
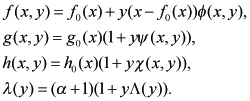 ---(2.5)
---(2.5)
Changing variable x to τ by
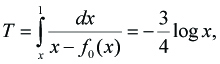 ---(2.6)
---(2.6)
The system (2.1)-(2.4) is transformed into
A(τ )Xτ (τ, y) + B(τ ) X (τ, y) − (α + 1)yIXy (τ, y) + Λ(y)q= yY(τ, y), X (0, y) = C (y),
Φ (τ, y) is bounded on τ, ------ (2.7)
for 0 < τ < ∞, 0 < y < 1. Here
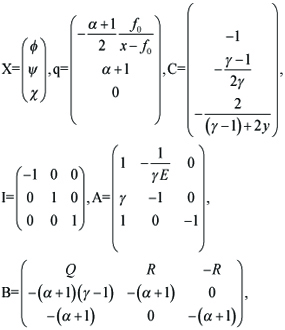 ----(2.8)
----(2.8)
where
Here the nonlinear term
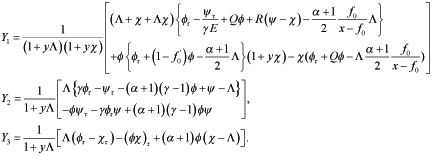 ----(2.9)
----(2.9)
The boundedness of Φ is required by (2.4).
For case (α, γ) = (2, 7), it follows that
E = 3/7, Q = 1, R = 3/4 -------(2.10)
where cofficients A, B in Eq.(2.7) are independent of τ.
Main Theorem
We here state the local existence for the system (2.1)-(2.4). The solution is prescribed as a fixed point of contractive mapping on a Banach space.
We here represent solution (X (τ, y), Λ(y)) of (2.7) as power series expansions in the form of
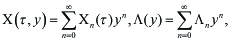 ----(3.1)
----(3.1)
for a given function Y(τ, y) of the form
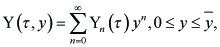 ----(3.2)
----(3.2)
for some ¯y ε (0, 1). Substituting into (2.7), the coefficients of yn satisfy the linear ordinary differential equation
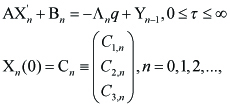 ----(3.3)
----(3.3)
where Cn the coefficient of expansion in y of C is given by
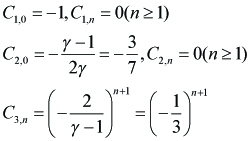 ----(3.4)
----(3.4)
and
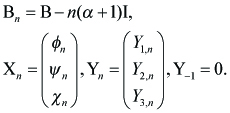 ----(3.5)
----(3.5)
We define a Banach space as follows. For τ ε (0,∞) and ¯y Ε (0,1), let
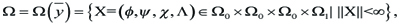 ----(3.6)
----(3.6)
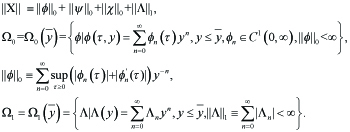 ----(3.7)
----(3.7)
We can easily see that Ω is a Banach space. For X ε Ω, let ˜X ε Ω be the solution of (2.7) with nonlinear term Y = Y(X) and let T : Ω −→ Ω be a mapping defined by ˜X = TX. The following lemma yields the unique existence of the fixed point of T.
Lemma 3.1 For R > 0 and ¯y ε (0, 1), let BR = {X ε Ω| ||X|| ≤ R}.
(i) There exist R0 > 0 and ¯y0 (R0) ε (0, 1) such that T(BR0) ⊂ BR0 .
(ii) T is contractive on BR0 , i.e., there exists a constant l ε (0, 1) such that
||TX1 − TX2|| ≤ l ||X1 − X2||
for all X1,X2 ε BR0.
See [3] for the proof.
Since the convergence of a solution is in y, the solution X (τ, y) is continuous in y. Thus our solution X (τ, y) tends to the similarity solution as y → 0.
Theorem 3.2 There exists a unique solution f (x, y) for the system (2.1)- (2.4), in [0, ¯y] for some ¯y ε (0, 1), which tends to the similarity solution (f0, g0, h0, λ(0)) as y → 0, provided that (α, γ) = (2, 7). Moreover it follows that
|f(x, y) − f0(x)| ≤ Cxy,
for any x ε (0, 1) and y ε (0, ¯y) with C = C(γ, f0).
Solution For The Transformed System
In parallel to [3], χn is given as
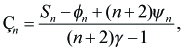 ----(4.1)
----(4.1)
where,
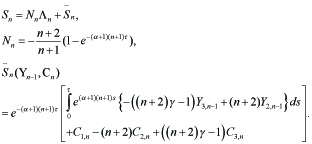 ----(4.2)
----(4.2)
For Un(τ ) = (φn(τ ), ψn(τ )), it follows that
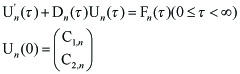 ----(4.3)
----(4.3)
Here,
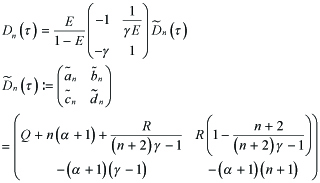 ---(4.4)
---(4.4)
and a nonhomogeneous term is of the form
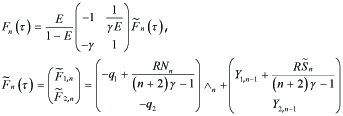 ---(4.5)
---(4.5)
In case (α, γ) = (2, 7),
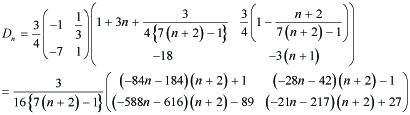 ---(4.6)
---(4.6)
We first recall the solution of
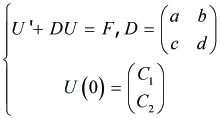 ---(4.7)
---(4.7)
provided that D satisfies (a + d)2 − 4(ad − bc) > 0.
Denoting
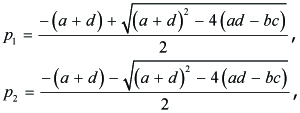 ---(4.8)
---(4.8)
fundamental solution Φ =
where
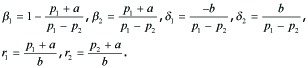 ---(4.9)
---(4.9)
For
it follows that
the solution of (4.7) is given by
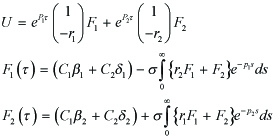 ---(4.10)
---(4.10)
In (4.6), (an + dn)2 − 4(andn − bncn) > 0 and p1p2 = andn − bncn < 0 for all n ε N, which yields p2 < 0 < p1. That is, we consider the condtion for the boundedness of | U | in (4.10), so that Φ(τ, y) in (2.7) is bounded on τ , provieded that ep1τ → ∞, ep2τ → 0 as τ → ∞. By p2 < 0, the boundedness of F1 and F2 yields | ep2τF2 |< ∞ since
< ∞. In order to apply to Fn in (4.5) later, for (4.7) letting
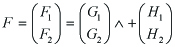 ------(4.11)
------(4.11)
we consider the condition of Λ which yields the boundedness of
| ep1τF1(τ ) |. We show the boundedness of | ep1τF1(τ ) |, provided that F1(∞) = 0 in (4.10). In fact, F1(∞) = 0 in (4.10) implies that
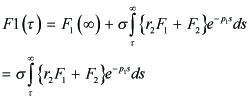 ------(4.12)
------(4.12)
Thus the boundedness of F1 and F2 yields | ep1τF1(τ ) |< ∞, since
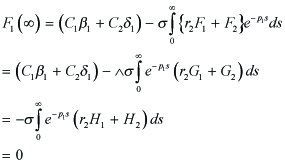 ----(4.13)
----(4.13)
this is,
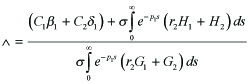 ----(4.14)
----(4.14)
Estimates for the Solution
In (4.6), we note that an, bn, cn, dn < 0 and an, bn, cn, dn = O(n) as n →∞, that is,is nonzero constant and so on for bn, cn, dn. For
p1,n > 0 > p2,n and p1,n, p2,n = O(n). Constants β1,n, β2,n, δ1,n, δ2,n are defined in parallel to (4.9) and satisfy
β1,n, β2,n, δ1,n > 0, δ2,n < 0
β1,n, β2,n = O(1), δ1,n, δ2,n = O(1),----(5.1)
that is, β1,n, β2,n, δ1,n, δ2,n are bounded with respect to n. For F1,n, F2,n in (4.5), Λn is defined as in (4.14). In parallel to (4.10) with (4.12), it follows that
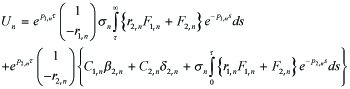 ----(5.2)
----(5.2)
where
σn = β1,nδ2,n − β2,nδ1,n = −δ1,n < 0, σn = O(1).-------(5.3)
r1,n, r2,n are also defined as in (4.9) and
r1,n, r2,n = O(1), r2,n > 0--------------------(5.4)
In case (α, γ) = (2, 7), (4.5) implies that Fn = GnΛn + Hn with
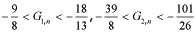 -------(5.5)
-------(5.5)
Applying inequality
with absolute constant C > 0 by (5.1), (5.3) and (5.5). Although p1,n can increase with order O(n), C1,n,C2,n = 0 for n ≥ 1 by (3.4), which implies that (|C1,n|+|C2,n|)p1,n is bounded. By (4.2), we see
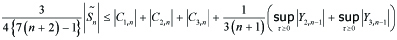 ---(5.6)
---(5.6)
which yields
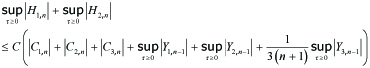 ---(5.7)
---(5.7)
We finally obtain
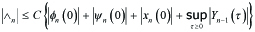 ---(5.8)
---(5.8)
By (5.2), it follows that
Since
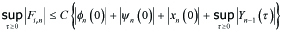 ------(5.9)
------(5.9)
We now obtain that
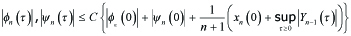 ------(5.10)
------(5.10)
Eq.(4.1) with (5.6), (5.8) and (5.10) yields
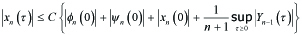 ------(5.11)
------(5.11)
Although Dn = O(n), noting (3.4), by (4.3) with (5.10) and (5.9), it follows that
By (3.3), we see
Here (n + 1)|χn(0)| is bounded by (3.4).
We conclude that
with absolute constant L1 and C. Here constant C depends only on Xn(0).
Eq.(2.5) implies that
for any x ε (0, 1) and y ε (0, ¯y) with C = C (α, γ, f0).
Conclusions
We has shown the existence of a solution for the system (2.1)- (2.4), provided that (α, γ) = (2, 7). The existence in this paper is local in y, i.e., in [0, ¯y] for some ¯y ε (0, 1) and the solution is continuous in y, namely, it tends to the similarity solution as y →0. The approximate solutioin is given exactly.
In order to consider this problem, it is usual to apply a hydrodynamic code. Since this result can be used as its exact initial condtion, we can use this result as an accuracy test to hydrodynamic code computations. Also we can utilize our results to consider the explosion in the water.
There are some more yet to be considered:
1. The problem of extending the present local solutions to a global one;
2. The existence of solution to the original gas dynamic equation in establishing its relation.
with the present solution of the basic equation (1.1), which is obtained by the blast wave transformation [4] or a hodograph transformation to the original equation.
Acknowledgments
The author would like to express his gratitude to Professor Akira Sakurai for his useful comments.
References
- Korobeinikov, V. P. (1991) Problems of Point-Blast Theory. American Institute of Physics.
- Morawetz, C. S. (1953) Perturbations about strong spherical shock waves. Institute for Mathe-matics and Mechanics, New York University No. 189.
- Takahashi, S. (2009) An existence theorem for the point source blast wave equation, Commun. Partial Differential Equations 34, 1–23.
- Sakurai, A., (1965) Blast Wave Theory. Basic Development in Fluid Dynamics, ed. Holt, Aca-demic Press 309–375.
- Sakurai, A.; Arai, T. (1982) On the existence of a solution of point source blast wave equation. Nagare 1,80–90 (In Japanese).
- Sedov, L. I. (1946) Motion of air in a strong blast. Dokl. Akad. Nauk SSSR52, No. 1, 17-20.
- Taylor, G. I. (1950) The formation of a blast wave by a very intense explosion II. The atomic explosion of 1945, Proc. Roy. Soc. A201, 175-186.





